
Question Number 9875 by j.masanja06@gmail.com last updated on 11/Jan/17
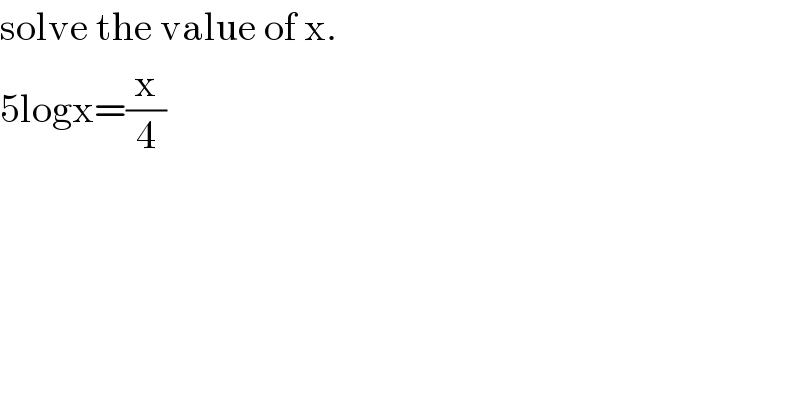
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\:\mathrm{x}. \\ $$$$\mathrm{5logx}=\frac{\mathrm{x}}{\mathrm{4}} \\ $$
Answered by mrW1 last updated on 12/Jan/17

$$\mathrm{5log}\:{x}=\frac{{x}}{\mathrm{4}} \\ $$$$\mathrm{log}\:{x}=\frac{{x}}{\mathrm{20}} \\ $$$$\frac{\mathrm{ln}\:{x}}{\mathrm{ln}\:\mathrm{10}}=\frac{{x}}{\mathrm{20}} \\ $$$$\mathrm{ln}\:{x}=\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{20}}{x} \\ $$$${with}\:{a}=−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{20}}\approx−\mathrm{0}.\mathrm{115129} \\ $$$$\mathrm{ln}\:{x}=−{ax} \\ $$$${x}={e}^{−{ax}} =\frac{\mathrm{1}}{{e}^{{ax}} } \\ $$$${xe}^{{ax}} =\mathrm{1} \\ $$$$\left({ax}\right){e}^{{ax}} ={a} \\ $$$$\Rightarrow{ax}={W}\left({a}\right) \\ $$$${with}\:{W}={Lambert}\:{W}\:{function} \\ $$$${x}=\frac{{W}\left({a}\right)}{{a}}=\frac{{W}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{20}}\right)}{−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{20}}}\approx\frac{{W}\left(−\mathrm{0}.\mathrm{115129}\right)}{−\mathrm{0}.\mathrm{115129}} \\ $$$$\approx\frac{−\mathrm{0}.\mathrm{13128}}{−\mathrm{0}.\mathrm{115129}}\approx\mathrm{1}.\mathrm{140286} \\ $$$${or} \\ $$$$\approx\frac{−\mathrm{3}.\mathrm{3794}}{−\mathrm{0}.\mathrm{115128}}\approx\mathrm{29}.\mathrm{35316} \\ $$
