
Question Number 115384 by mathdave last updated on 25/Sep/20
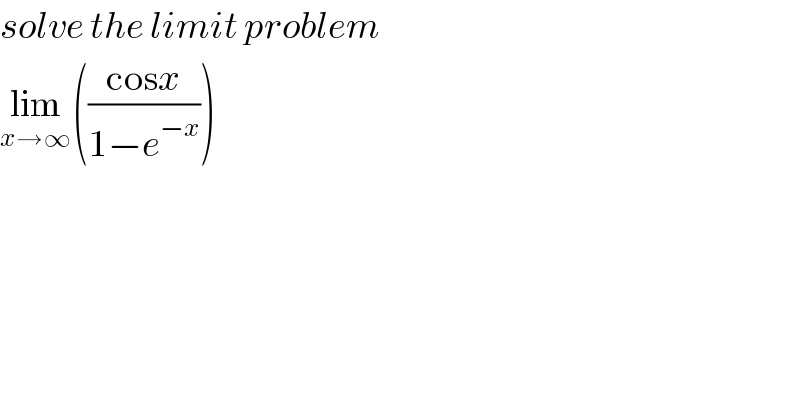
$${solve}\:{the}\:{limit}\:{problem} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{cos}{x}}{\mathrm{1}−{e}^{−{x}} }\right) \\ $$
Answered by MJS_new last updated on 25/Sep/20
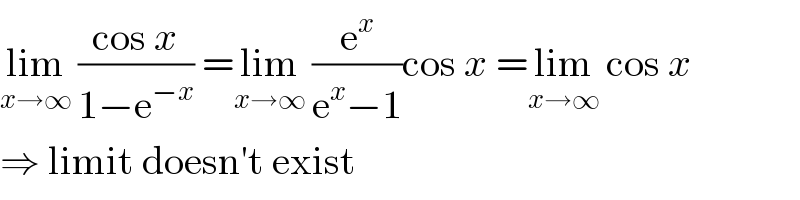
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{e}^{−{x}} }\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{e}^{{x}} }{\mathrm{e}^{{x}} −\mathrm{1}}\mathrm{cos}\:{x}\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{cos}\:{x} \\ $$$$\Rightarrow\:\mathrm{limit}\:\mathrm{doesn}'\mathrm{t}\:\mathrm{exist} \\ $$
