
Question Number 75938 by Rio Michael last updated on 21/Dec/19
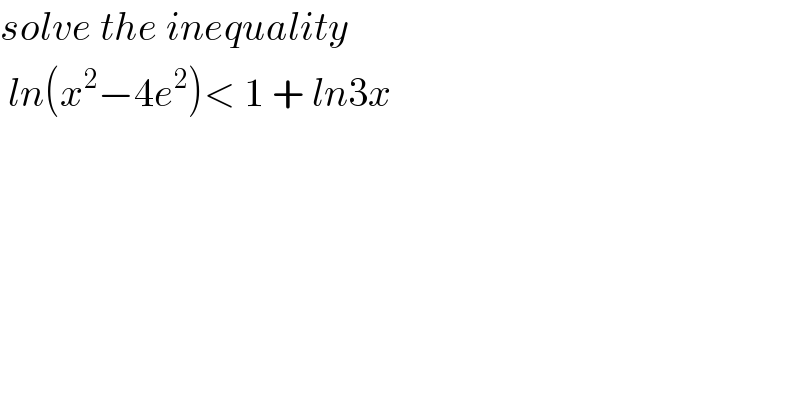
$${solve}\:{the}\:{inequality} \\ $$$$\:{ln}\left({x}^{\mathrm{2}} −\mathrm{4}{e}^{\mathrm{2}} \right)<\:\mathrm{1}\:+\:{ln}\mathrm{3}{x} \\ $$
Commented by turbo msup by abdo last updated on 21/Dec/19
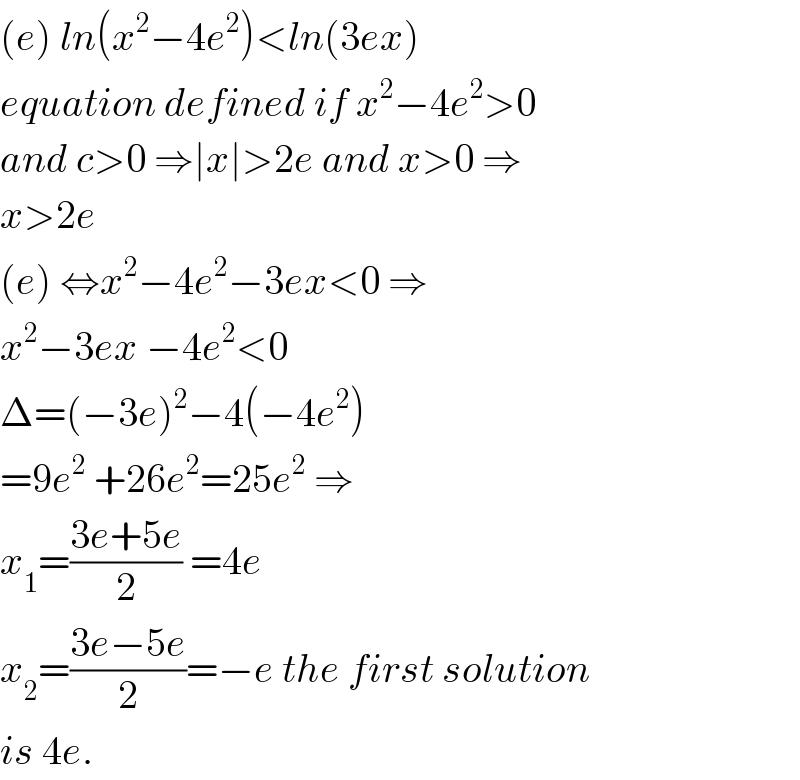
$$\left({e}\right)\:{ln}\left({x}^{\mathrm{2}} −\mathrm{4}{e}^{\mathrm{2}} \right)<{ln}\left(\mathrm{3}{ex}\right) \\ $$$${equation}\:{defined}\:{if}\:{x}^{\mathrm{2}} −\mathrm{4}{e}^{\mathrm{2}} >\mathrm{0}\: \\ $$$${and}\:{c}>\mathrm{0}\:\Rightarrow\mid{x}\mid>\mathrm{2}{e}\:{and}\:{x}>\mathrm{0}\:\Rightarrow \\ $$$${x}>\mathrm{2}{e} \\ $$$$\left({e}\right)\:\Leftrightarrow{x}^{\mathrm{2}} −\mathrm{4}{e}^{\mathrm{2}} −\mathrm{3}{ex}<\mathrm{0}\:\Rightarrow \\ $$$${x}^{\mathrm{2}} −\mathrm{3}{ex}\:−\mathrm{4}{e}^{\mathrm{2}} <\mathrm{0} \\ $$$$\Delta=\left(−\mathrm{3}{e}\right)^{\mathrm{2}} −\mathrm{4}\left(−\mathrm{4}{e}^{\mathrm{2}} \right) \\ $$$$=\mathrm{9}{e}^{\mathrm{2}} \:+\mathrm{26}{e}^{\mathrm{2}} =\mathrm{25}{e}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{3}{e}+\mathrm{5}{e}}{\mathrm{2}}\:=\mathrm{4}{e} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{3}{e}−\mathrm{5}{e}}{\mathrm{2}}=−{e}\:{the}\:{first}\:{solution} \\ $$$${is}\:\mathrm{4}{e}. \\ $$
Commented by Rio Michael last updated on 21/Dec/19

$${thanks} \\ $$
