
Question Number 27975 by NECx last updated on 18/Jan/18
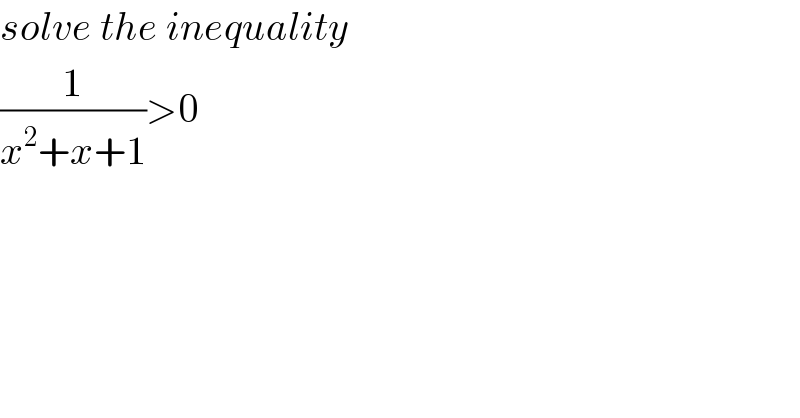
$${solve}\:{the}\:{inequality} \\ $$ $$\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}>\mathrm{0} \\ $$
Answered by mrW2 last updated on 18/Jan/18
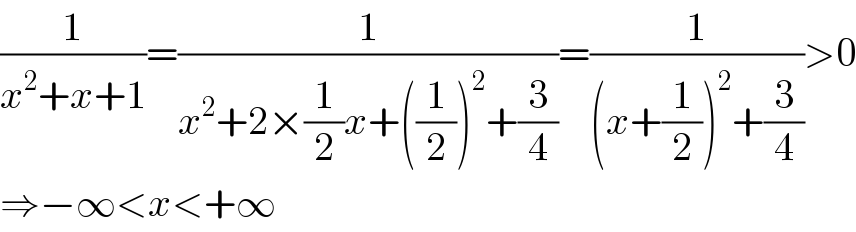
$$\frac{\mathrm{1}}{{x}^{\mathrm{2}} +{x}+\mathrm{1}}=\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}{x}+\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\mathrm{1}}{\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{4}}}>\mathrm{0} \\ $$ $$\Rightarrow−\infty<{x}<+\infty \\ $$
Commented byRasheed.Sindhi last updated on 18/Jan/18
N̸i̸c̸e̸ S̸i̸r̸!̸
