
Question Number 109734 by mathdave last updated on 25/Aug/20
![solve the following integral 1)∫_3 ^7 4(√((x−3)(7−x)))dx 2)∫_0 ^∞ ((xln^2 (1+x))/((1+x)^3 ))dx 3)∫_0 ^(π/4) [ln(1−tanx)]^2 dx=(π/2)ln2−2G 4)∫_0 ^(π/4) ln(1+cotx)dx=(π/8)ln2+G 5)∫_0 ^(π/2) ln(2+cosx)dx](Q109734.png)
$${solve}\:{the}\:{following}\:{integral} \\ $$$$\left.\mathrm{1}\right)\int_{\mathrm{3}} ^{\mathrm{7}} \mathrm{4}\sqrt{\left({x}−\mathrm{3}\right)\left(\mathrm{7}−{x}\right)}{dx} \\ $$$$\left.\mathrm{2}\right)\int_{\mathrm{0}} ^{\infty} \frac{{x}\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{3}} }{dx} \\ $$$$\left.\mathrm{3}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left[\mathrm{ln}\left(\mathrm{1}−\mathrm{tan}{x}\right)\right]^{\mathrm{2}} {dx}=\frac{\pi}{\mathrm{2}}\mathrm{ln2}−\mathrm{2}{G} \\ $$$$\left.\mathrm{4}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{ln}\left(\mathrm{1}+\mathrm{cot}{x}\right){dx}=\frac{\pi}{\mathrm{8}}\mathrm{ln2}+{G} \\ $$$$\left.\mathrm{5}\right)\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{ln}\left(\mathrm{2}+\mathrm{cos}{x}\right){dx} \\ $$
Answered by bobhans last updated on 25/Aug/20
![(1) ∫_3 ^7 4(√(4−(5−x)^2 )) dx = I let 5−x=2sin w → { ((w=π/2)),((w=−π/2)) :} I=∫_(π/2) ^(−π/2) 4(√(4−4sin^2 w)) (−2cos w dw) I= ∫_(−π/2) ^(π/2) 16 cos^2 w dw = 16∫_(−π/2) ^(π/2) ((1/2)+(1/2)cos 2w)dw =8[w+(1/2)sin 2w]_(−π/2) ^(π/2) = 8[π+0]=8π](Q109737.png)
$$\left(\mathrm{1}\right)\:\underset{\mathrm{3}} {\overset{\mathrm{7}} {\int}}\:\mathrm{4}\sqrt{\mathrm{4}−\left(\mathrm{5}−{x}\right)^{\mathrm{2}} }\:{dx}\:=\:{I} \\ $$$${let}\:\mathrm{5}−{x}=\mathrm{2sin}\:{w}\:\rightarrow\begin{cases}{{w}=\pi/\mathrm{2}}\\{{w}=−\pi/\mathrm{2}}\end{cases} \\ $$$${I}=\underset{\pi/\mathrm{2}} {\overset{−\pi/\mathrm{2}} {\int}}\mathrm{4}\sqrt{\mathrm{4}−\mathrm{4sin}\:^{\mathrm{2}} {w}}\:\left(−\mathrm{2cos}\:{w}\:{dw}\right) \\ $$$${I}=\:\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\mathrm{16}\:\mathrm{cos}\:^{\mathrm{2}} {w}\:{dw}\:=\:\mathrm{16}\underset{−\pi/\mathrm{2}} {\overset{\pi/\mathrm{2}} {\int}}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{2}{w}\right){dw} \\ $$$$=\mathrm{8}\left[{w}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}{w}\right]_{−\pi/\mathrm{2}} ^{\pi/\mathrm{2}} =\:\mathrm{8}\left[\pi+\mathrm{0}\right]=\mathrm{8}\pi \\ $$
Commented by mathdave last updated on 25/Aug/20
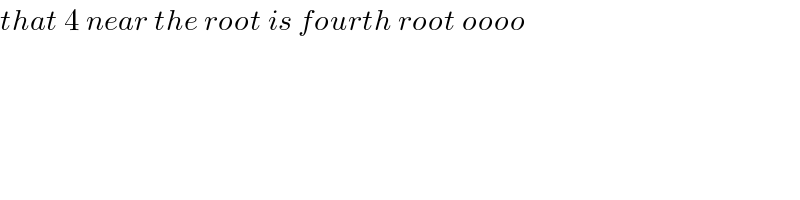
$${that}\:\mathrm{4}\:{near}\:{the}\:{root}\:{is}\:{fourth}\:{root}\:{oooo} \\ $$
