
Previous in Differential Equation Next in Differential Equation
Question Number 206449 by necx122 last updated on 15/Apr/24

$${solve}\:{the}\:{first}\:{order}\:{differential} \\ $$$${equation}: \\ $$$$ \\ $$$${xdy}\:−\:{ydx}\:=\:\left({xy}\right)^{\mathrm{1}/\mathrm{2}} {dx} \\ $$
Answered by Berbere last updated on 17/Apr/24
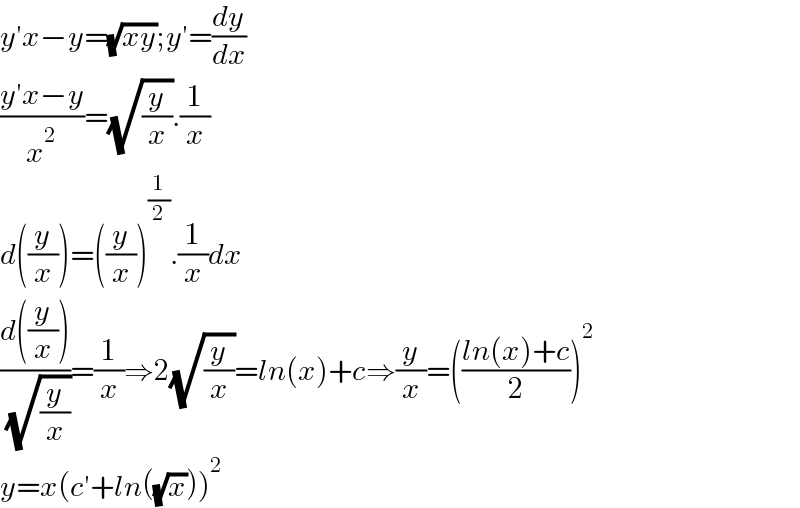
$${y}'{x}−{y}=\sqrt{{xy}};{y}'=\frac{{dy}}{{dx}} \\ $$$$\frac{{y}'{x}−{y}}{{x}^{\mathrm{2}} }=\sqrt{\frac{{y}}{{x}}}.\frac{\mathrm{1}}{{x}} \\ $$$${d}\left(\frac{{y}}{{x}}\right)=\left(\frac{{y}}{{x}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} .\frac{\mathrm{1}}{{x}}{dx} \\ $$$$\frac{{d}\left(\frac{{y}}{{x}}\right)}{\:\sqrt{\frac{{y}}{{x}}}}=\frac{\mathrm{1}}{{x}}\Rightarrow\mathrm{2}\sqrt{\frac{{y}}{{x}}}={ln}\left({x}\right)+{c}\Rightarrow\frac{{y}}{{x}}=\left(\frac{{ln}\left({x}\right)+{c}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$${y}={x}\left({c}'+{ln}\left(\sqrt{{x}}\right)\right)^{\mathrm{2}} \\ $$
Commented by necx122 last updated on 17/Apr/24
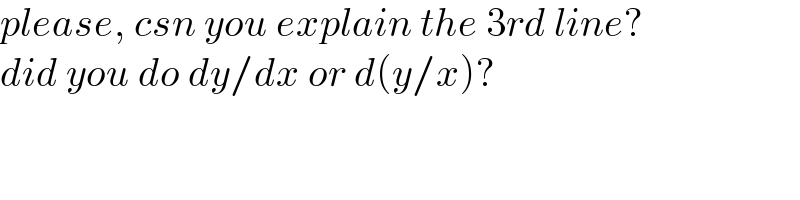
$${please},\:{csn}\:{you}\:{explain}\:{the}\:\mathrm{3}{rd}\:{line}? \\ $$$${did}\:{you}\:{do}\:{dy}/{dx}\:{or}\:{d}\left({y}/{x}\right)? \\ $$
Commented by Berbere last updated on 17/Apr/24
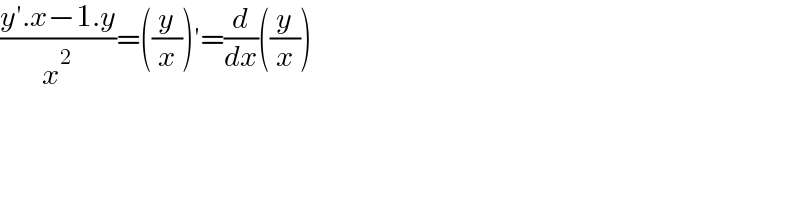
$$\frac{{y}'.{x}−\mathrm{1}.{y}}{{x}^{\mathrm{2}} }=\left(\frac{{y}}{{x}}\right)'=\frac{{d}}{{dx}}\left(\frac{{y}}{{x}}\right) \\ $$
Commented by necx122 last updated on 17/Apr/24
Thank you sir. It's clear now.
Commented by Berbere last updated on 18/Apr/24

$${withe}\:{Pleasur} \\ $$
