Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 188536 by normans last updated on 03/Mar/23

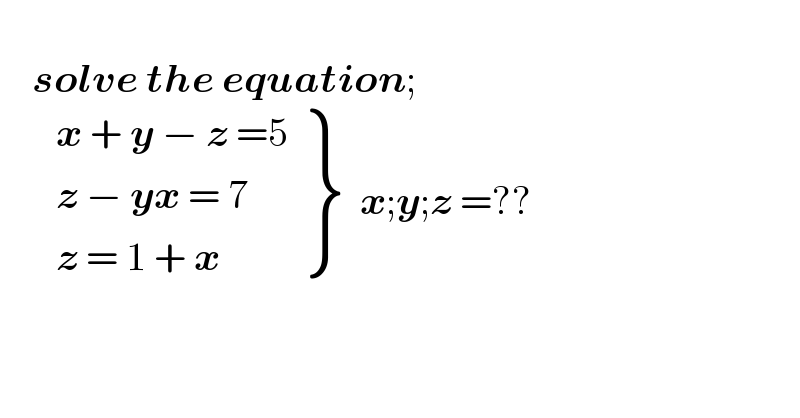
solve the equation; {: ((x + y − z =5)),((z − yx = 7)),((z = 1 + x)) } x;y;z =??

$$ \\ $$$$\:\:\:\:\boldsymbol{{solve}}\:\boldsymbol{{the}}\:\boldsymbol{{equation}}; \\ $$$$\:\:\:\:\:\:\:\left.\begin{matrix}{\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:−\:\boldsymbol{{z}}\:=\mathrm{5}}\\{\boldsymbol{{z}}\:−\:\boldsymbol{{yx}}\:=\:\mathrm{7}}\\{\boldsymbol{{z}}\:=\:\mathrm{1}\:+\:\boldsymbol{{x}}}\end{matrix}\right\}\:\:\boldsymbol{{x}};\boldsymbol{{y}};\boldsymbol{{z}}\:=??\:\:\:\:\:\: \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 03/Mar/23

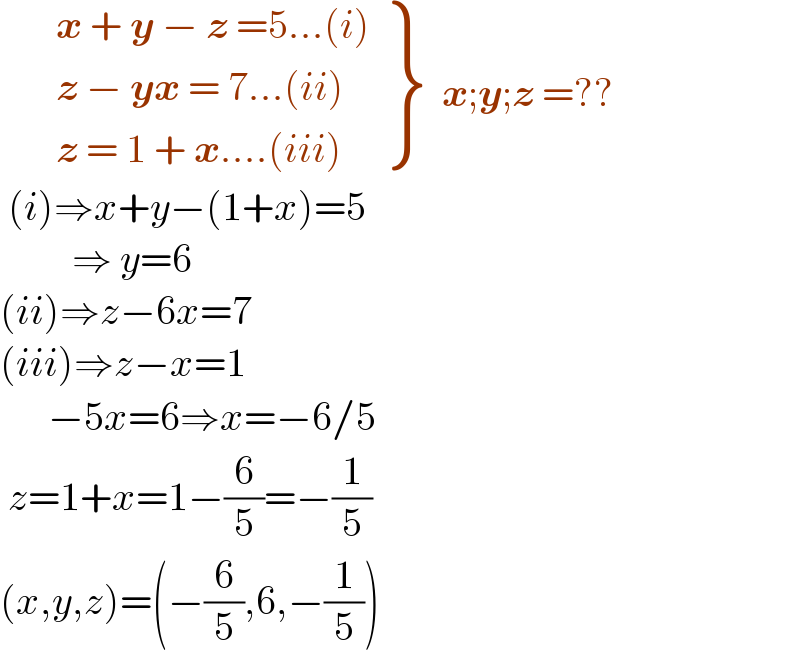
{: ((x + y − z =5...(i))),((z − yx = 7...(ii))),((z = 1 + x....(iii))) } x;y;z =?? (i)⇒x+y−(1+x)=5 ⇒ y=6 (ii)⇒z−6x=7 (iii)⇒z−x=1 −5x=6⇒x=−6/5 z=1+x=1−(6/5)=−(1/5) (x,y,z)=(−(6/5),6,−(1/5))

$$\:\:\:\:\:\:\:\left.\begin{matrix}{\boldsymbol{{x}}\:+\:\boldsymbol{{y}}\:−\:\boldsymbol{{z}}\:=\mathrm{5}...\left({i}\right)}\\{\boldsymbol{{z}}\:−\:\boldsymbol{{yx}}\:=\:\mathrm{7}...\left({ii}\right)}\\{\boldsymbol{{z}}\:=\:\mathrm{1}\:+\:\boldsymbol{{x}}....\left({iii}\right)}\end{matrix}\right\}\:\:\boldsymbol{{x}};\boldsymbol{{y}};\boldsymbol{{z}}\:=?? \\ $$$$\:\left({i}\right)\Rightarrow{x}+{y}−\left(\mathrm{1}+{x}\right)=\mathrm{5} \\ $$$$\:\:\:\:\:\:\:\:\:\Rightarrow\:{y}=\mathrm{6} \\ $$$$\left({ii}\right)\Rightarrow{z}−\mathrm{6}{x}=\mathrm{7} \\ $$$$\left({iii}\right)\Rightarrow{z}−{x}=\mathrm{1} \\ $$$$\:\:\:\:\:\:−\mathrm{5}{x}=\mathrm{6}\Rightarrow{x}=−\mathrm{6}/\mathrm{5} \\ $$$$\:{z}=\mathrm{1}+{x}=\mathrm{1}−\frac{\mathrm{6}}{\mathrm{5}}=−\frac{\mathrm{1}}{\mathrm{5}} \\ $$$$\left({x},{y},{z}\right)=\left(−\frac{\mathrm{6}}{\mathrm{5}},\mathrm{6},−\frac{\mathrm{1}}{\mathrm{5}}\right) \\ $$

Answered by Yhusuph last updated on 03/Mar/23

x+y−7−xy=5 x+y−xy=13......(i) x=((13−y)/(1−y))......(ii) 7+xy=1+x x−xy=6......(iii) x(1−y)=6 (((13−y)/(1−y)))(1−y)=6 13−y=6 y=7 x=(6/(1−y))=(6/(1−7))=−1 z= 1+x = 1+(−1)=0 ∴ x,y&z are −1,7 & 0 respectively ∂εηkεη la∫t βθrη

$${x}+{y}−\mathrm{7}−{xy}=\mathrm{5} \\ $$$${x}+{y}−{xy}=\mathrm{13}......\left({i}\right) \\ $$$${x}=\frac{\mathrm{13}−{y}}{\mathrm{1}−{y}}......\left({ii}\right) \\ $$$$\mathrm{7}+{xy}=\mathrm{1}+{x} \\ $$$${x}−{xy}=\mathrm{6}......\left({iii}\right) \\ $$$${x}\left(\mathrm{1}−{y}\right)=\mathrm{6} \\ $$$$\left(\frac{\mathrm{13}−{y}}{\mathrm{1}−{y}}\right)\left(\mathrm{1}−{y}\right)=\mathrm{6} \\ $$$$\mathrm{13}−{y}=\mathrm{6} \\ $$$${y}=\mathrm{7} \\ $$$${x}=\frac{\mathrm{6}}{\mathrm{1}−{y}}=\frac{\mathrm{6}}{\mathrm{1}−\mathrm{7}}=−\mathrm{1} \\ $$$${z}=\:\mathrm{1}+{x}\:=\:\mathrm{1}+\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$$\therefore\:{x},{y\&z}\:{are}\:−\mathrm{1},\mathrm{7}\:\&\:\mathrm{0}\:{respectively} \\ $$$$ \\ $$$$\partial\epsilon\eta{k}\epsilon\eta\:{la}\int{t}\:\beta\theta{r}\eta \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com