
Question Number 17576 by chux last updated on 07/Jul/17

$$\mathrm{solve}\:\mathrm{the}\:\mathrm{equation} \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{y}} =\mathrm{y}^{\mathrm{x}} .......\left(\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{2}} =\mathrm{y}^{\mathrm{3}} .......\left(\mathrm{2}\right) \\ $$
Answered by b.e.h.i.8.3.417@gmail.com last updated on 08/Jul/17
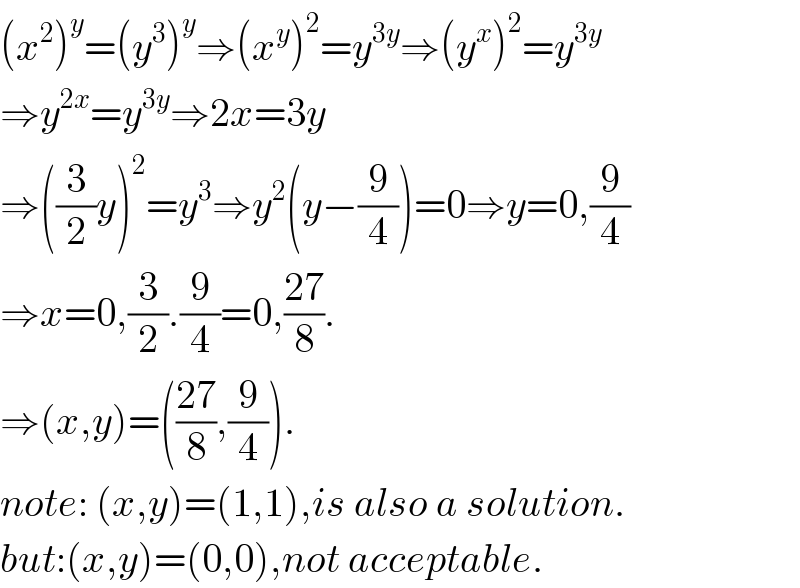
$$\left({x}^{\mathrm{2}} \right)^{{y}} =\left({y}^{\mathrm{3}} \right)^{{y}} \Rightarrow\left({x}^{{y}} \right)^{\mathrm{2}} ={y}^{\mathrm{3}{y}} \Rightarrow\left({y}^{{x}} \right)^{\mathrm{2}} ={y}^{\mathrm{3}{y}} \\ $$$$\Rightarrow{y}^{\mathrm{2}{x}} ={y}^{\mathrm{3}{y}} \Rightarrow\mathrm{2}{x}=\mathrm{3}{y} \\ $$$$\Rightarrow\left(\frac{\mathrm{3}}{\mathrm{2}}{y}\right)^{\mathrm{2}} ={y}^{\mathrm{3}} \Rightarrow{y}^{\mathrm{2}} \left({y}−\frac{\mathrm{9}}{\mathrm{4}}\right)=\mathrm{0}\Rightarrow{y}=\mathrm{0},\frac{\mathrm{9}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\mathrm{0},\frac{\mathrm{3}}{\mathrm{2}}.\frac{\mathrm{9}}{\mathrm{4}}=\mathrm{0},\frac{\mathrm{27}}{\mathrm{8}}. \\ $$$$\Rightarrow\left({x},{y}\right)=\left(\frac{\mathrm{27}}{\mathrm{8}},\frac{\mathrm{9}}{\mathrm{4}}\right). \\ $$$${note}:\:\left({x},{y}\right)=\left(\mathrm{1},\mathrm{1}\right),{is}\:{also}\:{a}\:{solution}. \\ $$$${but}:\left({x},{y}\right)=\left(\mathrm{0},\mathrm{0}\right),{not}\:{acceptable}. \\ $$
Commented by chux last updated on 08/Jul/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by chux last updated on 08/Jul/17
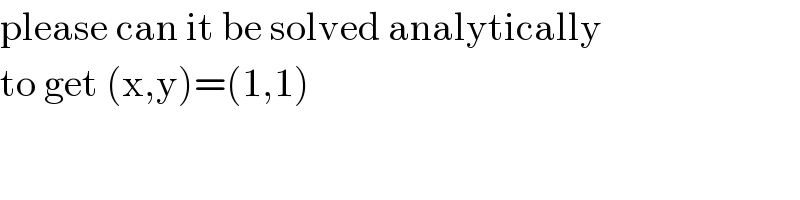
$$\mathrm{please}\:\mathrm{can}\:\mathrm{it}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{analytically} \\ $$$$\mathrm{to}\:\mathrm{get}\:\left(\mathrm{x},\mathrm{y}\right)=\left(\mathrm{1},\mathrm{1}\right) \\ $$
Commented by mrW1 last updated on 08/Jul/17
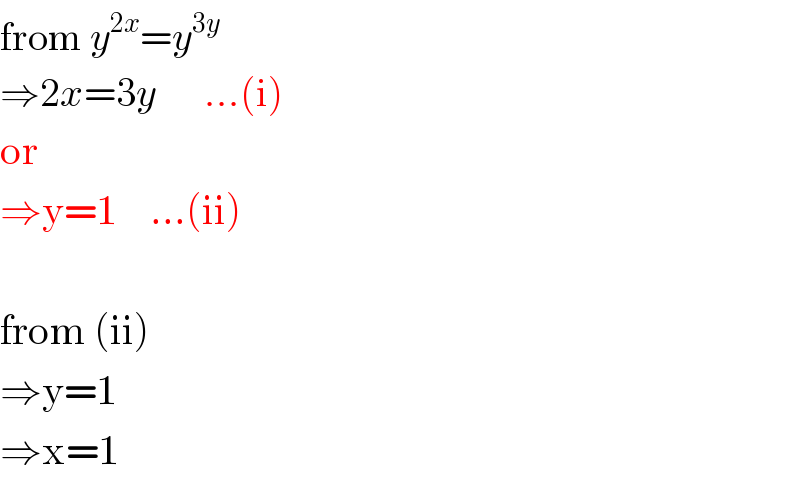
$$\mathrm{from}\:{y}^{\mathrm{2}{x}} ={y}^{\mathrm{3}{y}} \\ $$$$\Rightarrow\mathrm{2}{x}=\mathrm{3}{y}\:\:\:\:\:\:...\left(\mathrm{i}\right) \\ $$$$\mathrm{or} \\ $$$$\Rightarrow\mathrm{y}=\mathrm{1}\:\:\:\:...\left(\mathrm{ii}\right) \\ $$$$ \\ $$$$\mathrm{from}\:\left(\mathrm{ii}\right) \\ $$$$\Rightarrow\mathrm{y}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{1} \\ $$
Commented by chux last updated on 08/Jul/17

$$\mathrm{ok}....\:\mathrm{but}\:\mathrm{can}\:\mathrm{lambert}\:\mathrm{W}\:\mathrm{function} \\ $$$$\mathrm{solve}\:\mathrm{it}? \\ $$
Commented by mrW1 last updated on 09/Jul/17
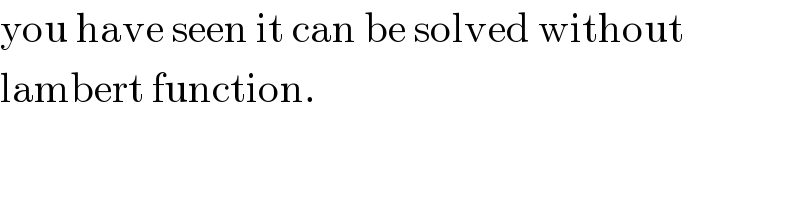
$$\mathrm{you}\:\mathrm{have}\:\mathrm{seen}\:\mathrm{it}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{without} \\ $$$$\mathrm{lambert}\:\mathrm{function}. \\ $$
Commented by chux last updated on 09/Jul/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
