
Question Number 132937 by mohammad17 last updated on 17/Feb/21
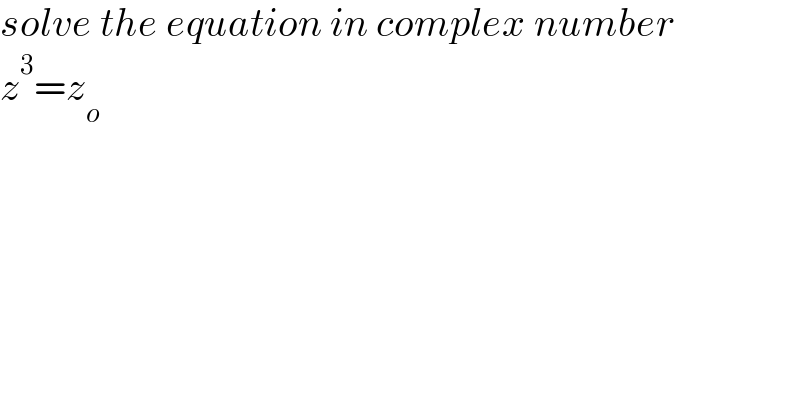
$${solve}\:{the}\:{equation}\:{in}\:{complex}\:{number} \\ $$$${z}^{\mathrm{3}} ={z}_{{o}} \\ $$
Answered by mr W last updated on 17/Feb/21
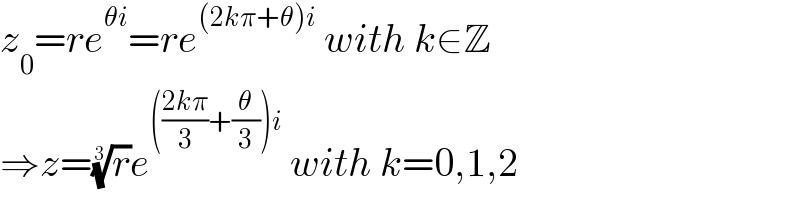
$${z}_{\mathrm{0}} ={re}^{\theta{i}} ={re}^{\left(\mathrm{2}{k}\pi+\theta\right){i}} \:{with}\:{k}\in\mathbb{Z} \\ $$$$\Rightarrow{z}=\sqrt[{\mathrm{3}}]{{r}}{e}^{\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\theta}{\mathrm{3}}\right){i}} \:{with}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$
Commented by mohammad17 last updated on 17/Feb/21
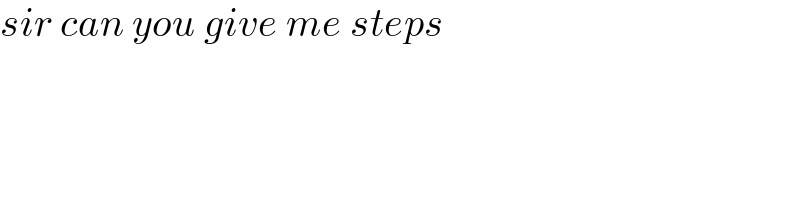
$${sir}\:{can}\:{you}\:{give}\:{me}\:{steps} \\ $$
Commented by mr W last updated on 17/Feb/21
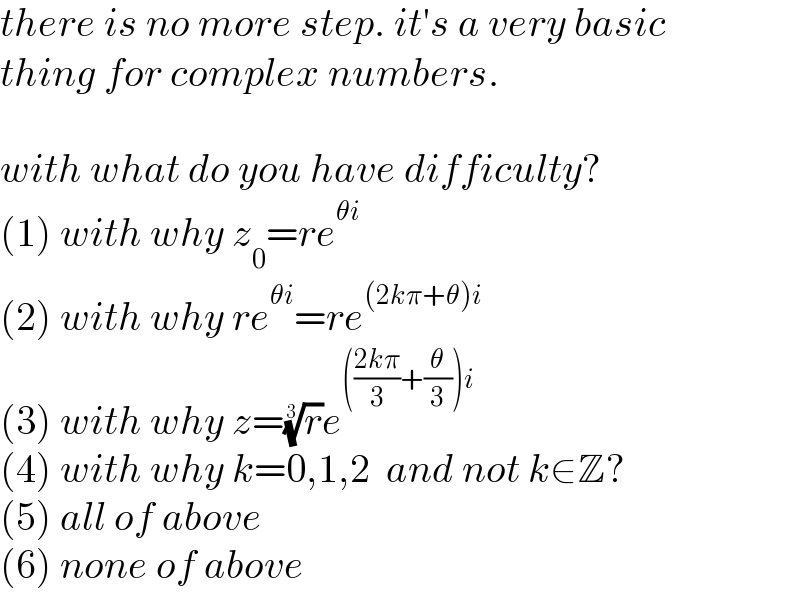
$${there}\:{is}\:{no}\:{more}\:{step}.\:{it}'{s}\:{a}\:{very}\:{basic} \\ $$$${thing}\:{for}\:{complex}\:{numbers}. \\ $$$$ \\ $$$${with}\:{what}\:{do}\:{you}\:{have}\:{difficulty}? \\ $$$$\left(\mathrm{1}\right)\:{with}\:{why}\:{z}_{\mathrm{0}} ={re}^{\theta{i}} \\ $$$$\left(\mathrm{2}\right)\:{with}\:{why}\:{re}^{\theta{i}} ={re}^{\left(\mathrm{2}{k}\pi+\theta\right){i}} \\ $$$$\left(\mathrm{3}\right)\:{with}\:{why}\:{z}=\sqrt[{\mathrm{3}}]{{r}}{e}^{\left(\frac{\mathrm{2}{k}\pi}{\mathrm{3}}+\frac{\theta}{\mathrm{3}}\right){i}} \\ $$$$\left(\mathrm{4}\right)\:{with}\:{why}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2}\:\:{and}\:{not}\:{k}\in\mathbb{Z}? \\ $$$$\left(\mathrm{5}\right)\:{all}\:{of}\:{above} \\ $$$$\left(\mathrm{6}\right)\:{none}\:{of}\:{above} \\ $$
