
Question Number 162959 by mkam last updated on 02/Jan/22
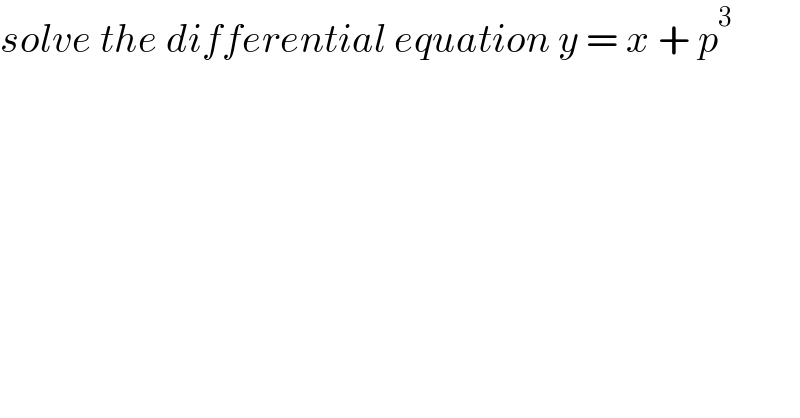
$${solve}\:{the}\:{differential}\:{equation}\:{y}\:=\:{x}\:+\:{p}^{\mathrm{3}} \\ $$
Commented by mr W last updated on 02/Jan/22
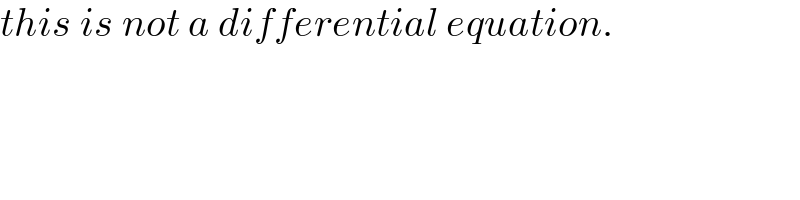
$${this}\:{is}\:{not}\:{a}\:{differential}\:{equation}. \\ $$
Commented by Kamel last updated on 02/Jan/22

$${Mr}\:{W}\:{p}=\frac{{dy}}{{dx}}. \\ $$
Commented by mr W last updated on 02/Jan/22
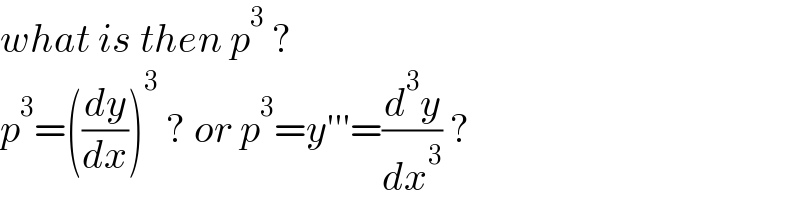
$${what}\:{is}\:{then}\:{p}^{\mathrm{3}} \:? \\ $$$${p}^{\mathrm{3}} =\left(\frac{{dy}}{{dx}}\right)^{\mathrm{3}} \:?\:{or}\:{p}^{\mathrm{3}} ={y}'''=\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }\:? \\ $$
Commented by Kamel last updated on 02/Jan/22
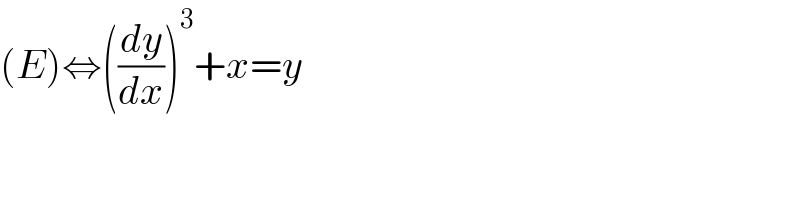
$$\left({E}\right)\Leftrightarrow\left(\frac{{dy}}{{dx}}\right)^{\mathrm{3}} +{x}={y} \\ $$
Commented by mkam last updated on 02/Jan/22

$${yes}\:{sir} \\ $$
Answered by mr W last updated on 02/Jan/22
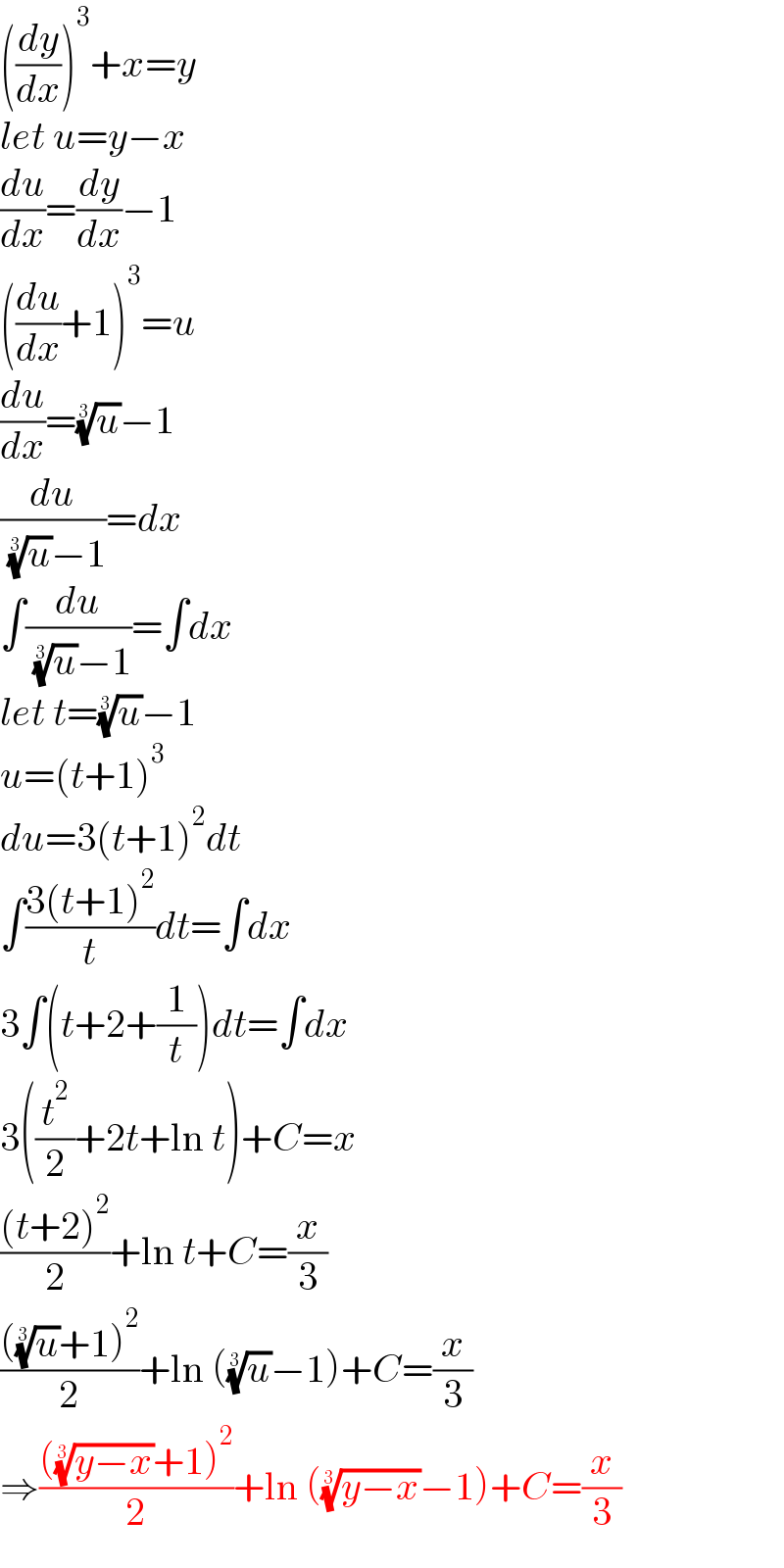
$$\left(\frac{{dy}}{{dx}}\right)^{\mathrm{3}} +{x}={y} \\ $$$${let}\:{u}={y}−{x} \\ $$$$\frac{{du}}{{dx}}=\frac{{dy}}{{dx}}−\mathrm{1} \\ $$$$\left(\frac{{du}}{{dx}}+\mathrm{1}\right)^{\mathrm{3}} ={u} \\ $$$$\frac{{du}}{{dx}}=\sqrt[{\mathrm{3}}]{{u}}−\mathrm{1} \\ $$$$\frac{{du}}{\:\sqrt[{\mathrm{3}}]{{u}}−\mathrm{1}}={dx} \\ $$$$\int\frac{{du}}{\:\sqrt[{\mathrm{3}}]{{u}}−\mathrm{1}}=\int{dx} \\ $$$${let}\:{t}=\sqrt[{\mathrm{3}}]{{u}}−\mathrm{1} \\ $$$${u}=\left({t}+\mathrm{1}\right)^{\mathrm{3}} \\ $$$${du}=\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{2}} {dt} \\ $$$$\int\frac{\mathrm{3}\left({t}+\mathrm{1}\right)^{\mathrm{2}} }{{t}}{dt}=\int{dx} \\ $$$$\mathrm{3}\int\left({t}+\mathrm{2}+\frac{\mathrm{1}}{{t}}\right){dt}=\int{dx} \\ $$$$\mathrm{3}\left(\frac{{t}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{t}+\mathrm{ln}\:{t}\right)+{C}={x} \\ $$$$\frac{\left({t}+\mathrm{2}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{ln}\:{t}+{C}=\frac{{x}}{\mathrm{3}} \\ $$$$\frac{\left(\sqrt[{\mathrm{3}}]{{u}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{{u}}−\mathrm{1}\right)+{C}=\frac{{x}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\left(\sqrt[{\mathrm{3}}]{{y}−{x}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{2}}+\mathrm{ln}\:\left(\sqrt[{\mathrm{3}}]{{y}−{x}}−\mathrm{1}\right)+{C}=\frac{{x}}{\mathrm{3}} \\ $$
Commented by Kamel last updated on 02/Jan/22
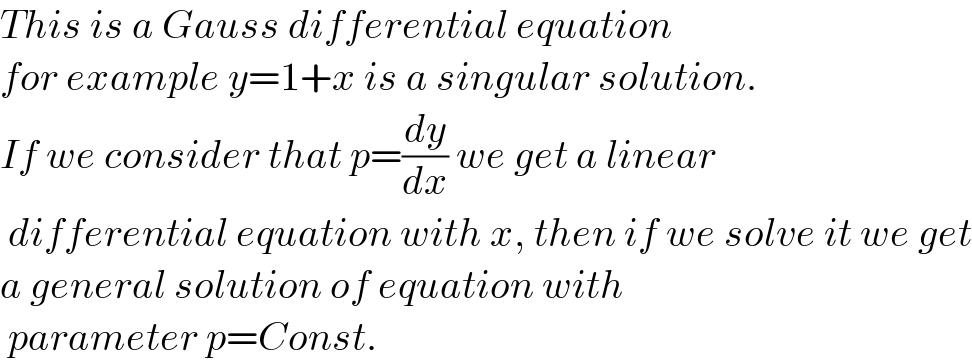
$${This}\:{is}\:{a}\:{Gauss}\:{differential}\:{equation} \\ $$$${for}\:{example}\:{y}=\mathrm{1}+{x}\:{is}\:{a}\:{singular}\:{solution}. \\ $$$${If}\:{we}\:{consider}\:{that}\:{p}=\frac{{dy}}{{dx}}\:{we}\:{get}\:{a}\:{linear} \\ $$$$\:{differential}\:{equation}\:{with}\:{x},\:{then}\:{if}\:{we}\:{solve}\:{it}\:{we}\:{get} \\ $$$${a}\:{general}\:{solution}\:{of}\:{equation}\:{with} \\ $$$$\:{parameter}\:{p}={Const}. \\ $$
Commented by mr W last updated on 02/Jan/22

$${i}\:{don}'{t}\:{understand}\:{that}\:{much}.\:{what} \\ $$$${is}\:{then}\:{the}\:{solution}?\:{is}\:{anything} \\ $$$${wrong}\:{in}\:{my}\:{solution}? \\ $$
Commented by Kamel last updated on 02/Jan/22

$${No},\:{it}'{s}\:{correct}.\: \\ $$
Commented by mr W last updated on 02/Jan/22
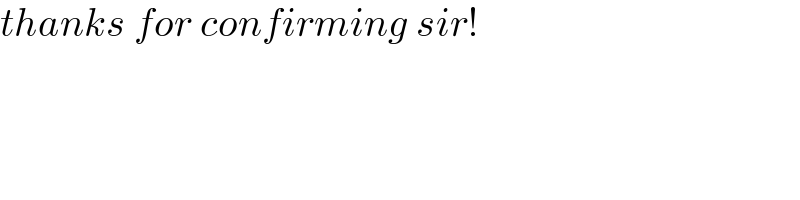
$${thanks}\:{for}\:{confirming}\:{sir}! \\ $$
