
Question Number 128903 by Engr_Jidda last updated on 11/Jan/21

$${solve}\:{the}\:{differential}\:{equation} \\ $$$$\frac{{dy}^{\mathrm{2}} }{{dx}^{\mathrm{2}\:} }+{y}=\mathrm{0} \\ $$
Answered by mindispower last updated on 11/Jan/21
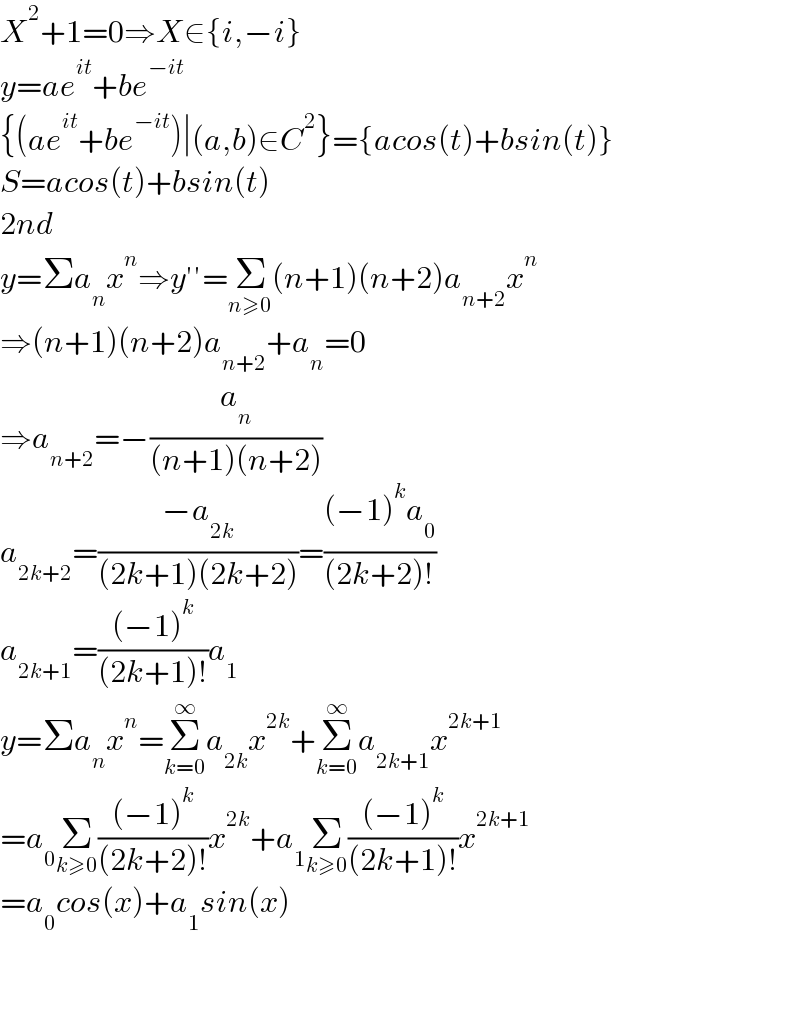
$${X}^{\mathrm{2}} +\mathrm{1}=\mathrm{0}\Rightarrow{X}\in\left\{{i},−{i}\right\} \\ $$$${y}={ae}^{{it}} +{be}^{−{it}} \\ $$$$\left\{\left({ae}^{{it}} +{be}^{−{it}} \right)\mid\left({a},{b}\right)\in{C}^{\mathrm{2}} \right\}=\left\{{acos}\left({t}\right)+{bsin}\left({t}\right)\right\} \\ $$$${S}={acos}\left({t}\right)+{bsin}\left({t}\right) \\ $$$$\mathrm{2}{nd}\: \\ $$$${y}=\Sigma{a}_{{n}} {x}^{{n}} \Rightarrow{y}''=\underset{{n}\geqslant\mathrm{0}} {\sum}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){a}_{{n}+\mathrm{2}} {x}^{{n}} \\ $$$$\Rightarrow\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right){a}_{{n}+\mathrm{2}} +{a}_{{n}} =\mathrm{0} \\ $$$$\Rightarrow{a}_{{n}+\mathrm{2}} =−\frac{{a}_{{n}} }{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)} \\ $$$${a}_{\mathrm{2}{k}+\mathrm{2}} =\frac{−{a}_{\mathrm{2}{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)\left(\mathrm{2}{k}+\mathrm{2}\right)}=\frac{\left(−\mathrm{1}\right)^{{k}} {a}_{\mathrm{0}} }{\left(\mathrm{2}{k}+\mathrm{2}\right)!} \\ $$$${a}_{\mathrm{2}{k}+\mathrm{1}} =\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!}{a}_{\mathrm{1}} \\ $$$${y}=\Sigma{a}_{{n}} {x}^{{n}} =\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{\mathrm{2}{k}} {x}^{\mathrm{2}{k}} +\underset{{k}=\mathrm{0}} {\overset{\infty} {\sum}}{a}_{\mathrm{2}{k}+\mathrm{1}} {x}^{\mathrm{2}{k}+\mathrm{1}} \\ $$$$={a}_{\mathrm{0}} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}{k}+\mathrm{2}\right)!}{x}^{\mathrm{2}{k}} +{a}_{\mathrm{1}} \underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}} }{\left(\mathrm{2}{k}+\mathrm{1}\right)!}{x}^{\mathrm{2}{k}+\mathrm{1}} \\ $$$$={a}_{\mathrm{0}} {cos}\left({x}\right)+{a}_{\mathrm{1}} {sin}\left({x}\right) \\ $$$$ \\ $$$$ \\ $$
Answered by Olaf last updated on 11/Jan/21
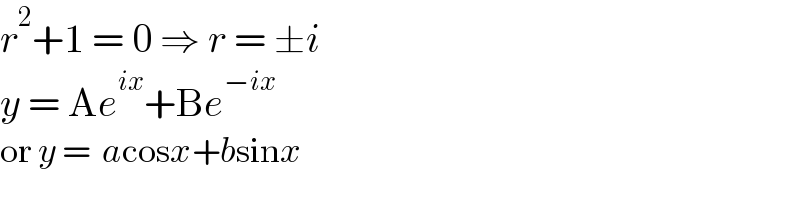
$${r}^{\mathrm{2}} +\mathrm{1}\:=\:\mathrm{0}\:\Rightarrow\:{r}\:=\:\pm{i} \\ $$$${y}\:=\:\mathrm{A}{e}^{{ix}} +\mathrm{B}{e}^{−{ix}} \\ $$$$\mathrm{or}\:{y}\:=\:\:{a}\mathrm{cos}{x}+{b}\mathrm{sin}{x} \\ $$
