
Previous in Relation and Functions Next in Relation and Functions
Question Number 65402 by mathmax by abdo last updated on 29/Jul/19
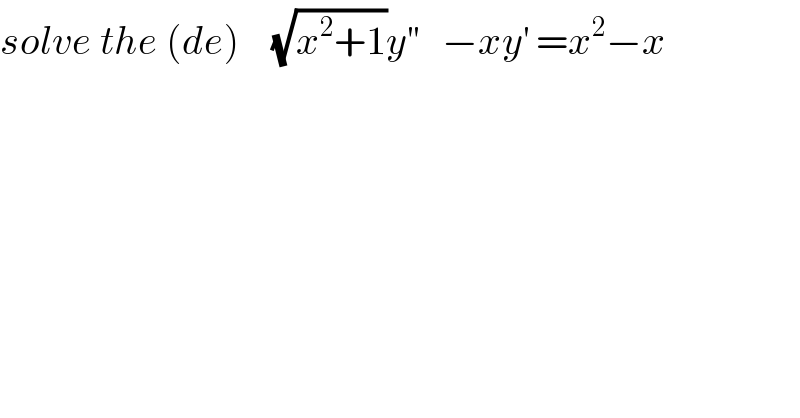
$${solve}\:{the}\:\left({de}\right)\:\:\:\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{y}^{''} \:\:\:−{xy}^{'} \:={x}^{\mathrm{2}} −{x} \\ $$
Commented by mathmax by abdo last updated on 30/Jul/19
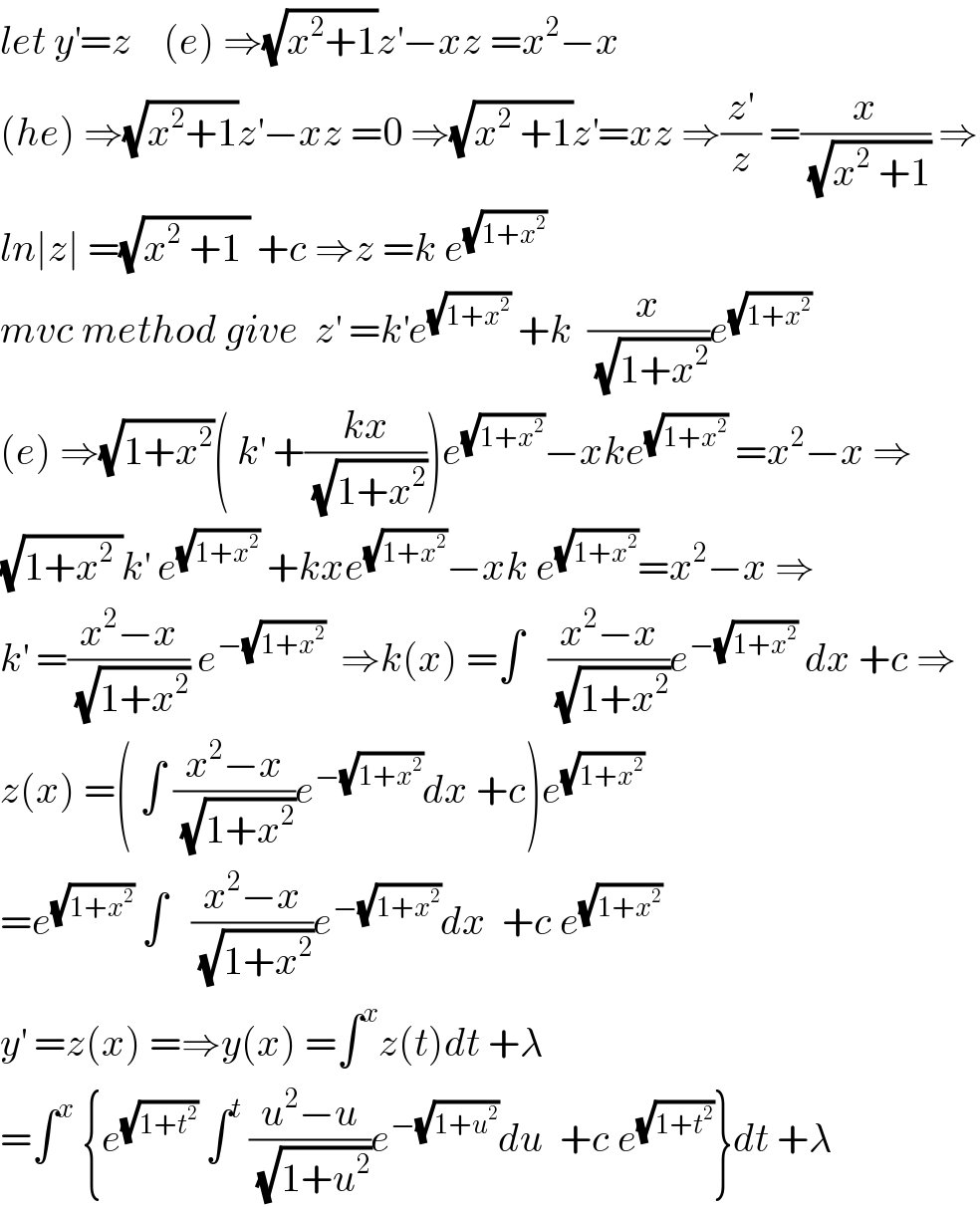
$${let}\:{y}^{'} ={z}\:\:\:\:\left({e}\right)\:\Rightarrow\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{z}^{'} −{xz}\:={x}^{\mathrm{2}} −{x} \\ $$$$\left({he}\right)\:\Rightarrow\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}{z}^{'} −{xz}\:=\mathrm{0}\:\Rightarrow\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}{z}^{'} ={xz}\:\Rightarrow\frac{{z}^{'} }{{z}}\:=\frac{{x}}{\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}}}\:\Rightarrow \\ $$$${ln}\mid{z}\mid\:=\sqrt{{x}^{\mathrm{2}} \:+\mathrm{1}\:}\:+{c}\:\Rightarrow{z}\:={k}\:{e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${mvc}\:{method}\:{give}\:\:{z}^{'} \:={k}^{'} {e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \:+{k}\:\:\frac{{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$\left({e}\right)\:\Rightarrow\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\left(\:{k}^{'} \:+\frac{{kx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\right){e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} −{xke}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \:={x}^{\mathrm{2}} −{x}\:\Rightarrow \\ $$$$\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}{k}^{'} \:{e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \:+{kxe}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} −{xk}\:{e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} ={x}^{\mathrm{2}} −{x}\:\Rightarrow \\ $$$${k}^{'} \:=\frac{{x}^{\mathrm{2}} −{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{e}^{−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \:\:\Rightarrow{k}\left({x}\right)\:=\int\:\:\:\frac{{x}^{\mathrm{2}} −{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{e}^{−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \:{dx}\:+{c}\:\Rightarrow \\ $$$${z}\left({x}\right)\:=\left(\:\int\:\frac{{x}^{\mathrm{2}} −{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{e}^{−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} {dx}\:+{c}\right){e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$$={e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \:\int\:\:\:\frac{{x}^{\mathrm{2}} −{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{e}^{−\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} {dx}\:\:+{c}\:{e}^{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${y}^{'} \:={z}\left({x}\right)\:=\Rightarrow{y}\left({x}\right)\:=\int^{{x}} {z}\left({t}\right){dt}\:+\lambda \\ $$$$=\int^{{x}} \:\left\{{e}^{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \:\int^{{t}} \:\frac{{u}^{\mathrm{2}} −{u}}{\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}{e}^{−\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }} {du}\:\:+{c}\:{e}^{\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }} \right\}{dt}\:+\lambda\: \\ $$
