
Previous in Differential Equation Next in Differential Equation
Question Number 200022 by jlewis last updated on 12/Nov/23
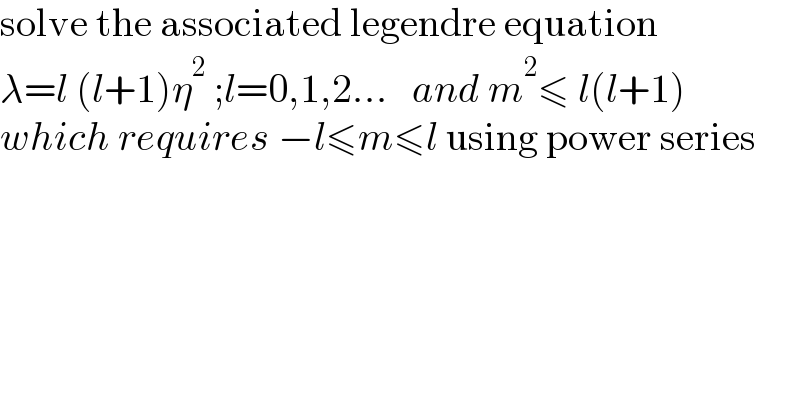
$$\mathrm{solve}\:\mathrm{the}\:\mathrm{associated}\:\mathrm{legendre}\:\mathrm{equation} \\ $$$$\lambda={l}\:\left({l}+\mathrm{1}\right)\eta^{\mathrm{2}} \:;{l}=\mathrm{0},\mathrm{1},\mathrm{2}...\:\:\:{and}\:{m}^{\mathrm{2}} \leqslant\:{l}\left({l}+\mathrm{1}\right)\: \\ $$$${which}\:{requires}\:−{l}\leqslant{m}\leqslant{l}\:\mathrm{using}\:\mathrm{power}\:\mathrm{series} \\ $$
