
Previous in Relation and Functions Next in Relation and Functions
Question Number 37296 by math khazana by abdo last updated on 11/Jun/18
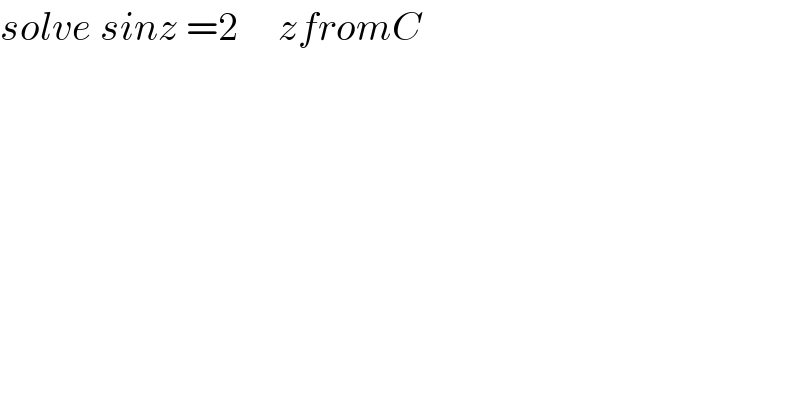
$${solve}\:{sinz}\:=\mathrm{2}\:\:\:\:\:{zfromC} \\ $$$$ \\ $$
Commented by prof Abdo imad last updated on 17/Jun/18
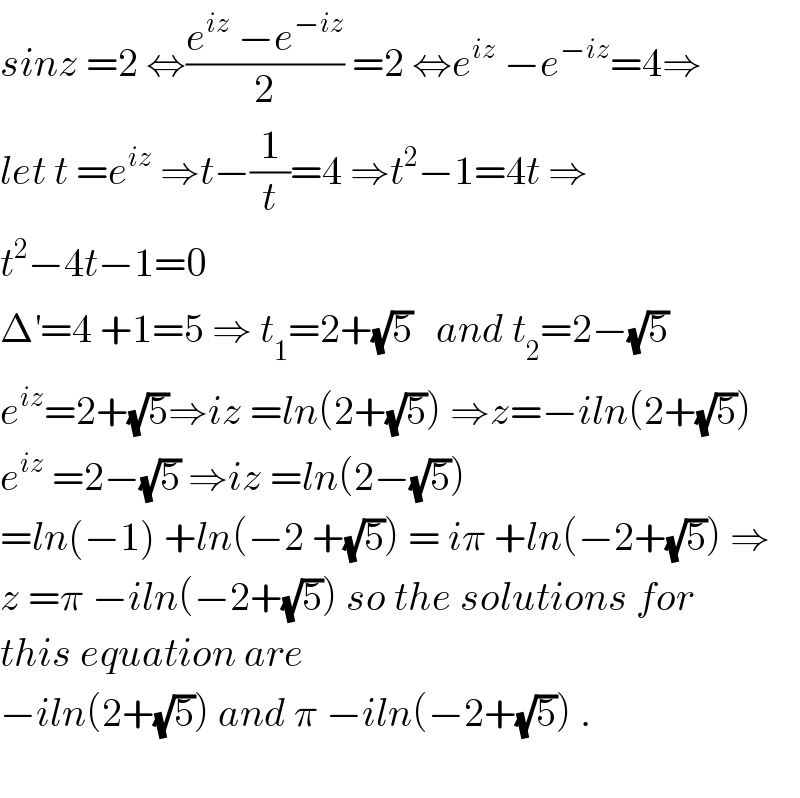
$${sinz}\:=\mathrm{2}\:\Leftrightarrow\frac{{e}^{{iz}} \:−{e}^{−{iz}} }{\mathrm{2}}\:=\mathrm{2}\:\Leftrightarrow{e}^{{iz}} \:−{e}^{−{iz}} =\mathrm{4}\Rightarrow \\ $$$${let}\:{t}\:={e}^{{iz}} \:\Rightarrow{t}−\frac{\mathrm{1}}{{t}}=\mathrm{4}\:\Rightarrow{t}^{\mathrm{2}} −\mathrm{1}=\mathrm{4}{t}\:\Rightarrow \\ $$$${t}^{\mathrm{2}} −\mathrm{4}{t}−\mathrm{1}=\mathrm{0}\: \\ $$$$\Delta^{'} =\mathrm{4}\:+\mathrm{1}=\mathrm{5}\:\Rightarrow\:{t}_{\mathrm{1}} =\mathrm{2}+\sqrt{\mathrm{5}}\:\:\:{and}\:{t}_{\mathrm{2}} =\mathrm{2}−\sqrt{\mathrm{5}} \\ $$$${e}^{{iz}} =\mathrm{2}+\sqrt{\mathrm{5}}\Rightarrow{iz}\:={ln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\:\Rightarrow{z}=−{iln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right) \\ $$$${e}^{{iz}} \:=\mathrm{2}−\sqrt{\mathrm{5}}\:\Rightarrow{iz}\:={ln}\left(\mathrm{2}−\sqrt{\mathrm{5}}\right) \\ $$$$={ln}\left(−\mathrm{1}\right)\:+{ln}\left(−\mathrm{2}\:+\sqrt{\mathrm{5}}\right)\:=\:{i}\pi\:+{ln}\left(−\mathrm{2}+\sqrt{\mathrm{5}}\right)\:\Rightarrow \\ $$$${z}\:=\pi\:−{iln}\left(−\mathrm{2}+\sqrt{\mathrm{5}}\right)\:{so}\:{the}\:{solutions}\:{for} \\ $$$${this}\:{equation}\:{are} \\ $$$$−{iln}\left(\mathrm{2}+\sqrt{\mathrm{5}}\right)\:{and}\:\pi\:−{iln}\left(−\mathrm{2}+\sqrt{\mathrm{5}}\right)\:. \\ $$$$ \\ $$
