
Question Number 103089 by M±th+et+s last updated on 12/Jul/20
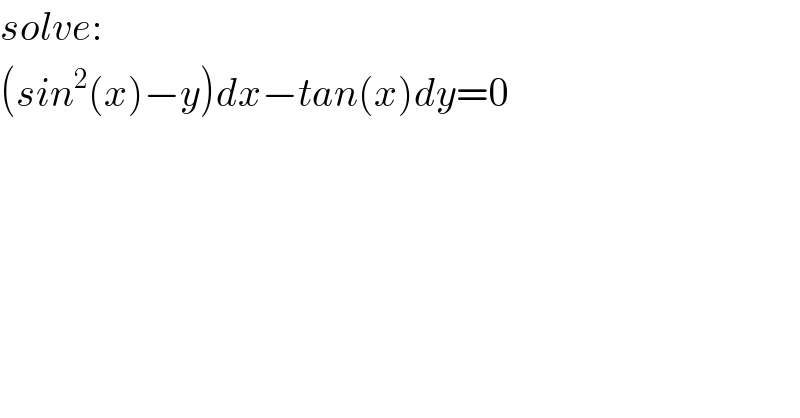
$${solve}: \\ $$$$\left({sin}^{\mathrm{2}} \left({x}\right)−{y}\right){dx}−{tan}\left({x}\right){dy}=\mathrm{0} \\ $$
Answered by Ar Brandon last updated on 12/Jul/20
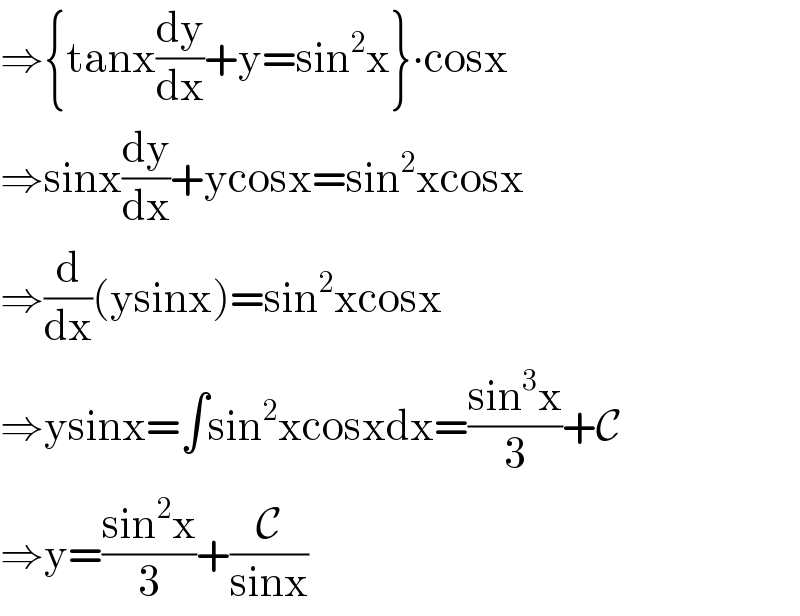
$$\Rightarrow\left\{\mathrm{tanx}\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{y}=\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right\}\centerdot\mathrm{cosx} \\ $$$$\Rightarrow\mathrm{sinx}\frac{\mathrm{dy}}{\mathrm{dx}}+\mathrm{ycosx}=\mathrm{sin}^{\mathrm{2}} \mathrm{xcosx} \\ $$$$\Rightarrow\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{ysinx}\right)=\mathrm{sin}^{\mathrm{2}} \mathrm{xcosx} \\ $$$$\Rightarrow\mathrm{ysinx}=\int\mathrm{sin}^{\mathrm{2}} \mathrm{xcosxdx}=\frac{\mathrm{sin}^{\mathrm{3}} \mathrm{x}}{\mathrm{3}}+\mathcal{C} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}{\mathrm{3}}+\frac{\mathcal{C}}{\mathrm{sinx}} \\ $$
