
Question Number 115812 by mathdave last updated on 28/Sep/20
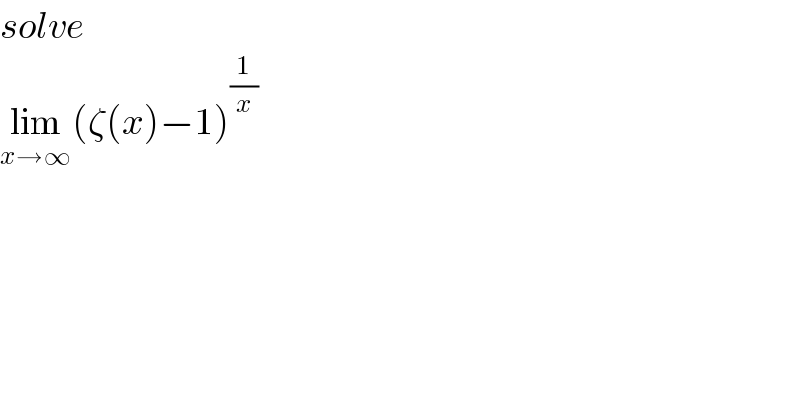
$${solve} \\ $$$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\zeta\left({x}\right)−\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}}} \\ $$
Commented by Dwaipayan Shikari last updated on 28/Sep/20
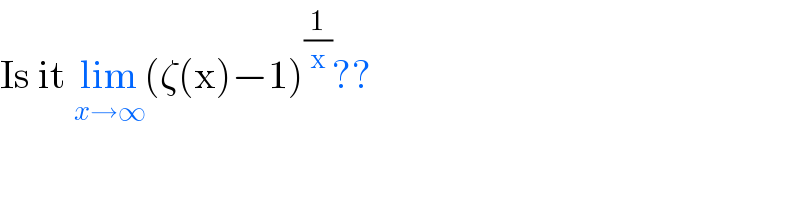
$$\mathrm{Is}\:\mathrm{it}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\zeta\left(\mathrm{x}\right)−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} ?? \\ $$
Commented by mathdave last updated on 28/Sep/20

$${yes}\:{any}\:{idea} \\ $$
Commented by Dwaipayan Shikari last updated on 28/Sep/20
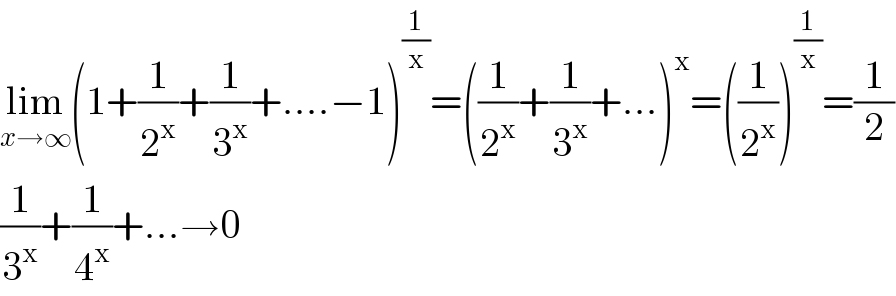
$$\underset{{x}\rightarrow\infty} {\mathrm{lim}}\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{x}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }+....−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{x}}} =\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{x}} }+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }+...\right)^{\mathrm{x}} =\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{x}} }\right)^{\frac{\mathrm{1}}{\mathrm{x}}} =\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{x}} }+...\rightarrow\mathrm{0} \\ $$
Commented by Dwaipayan Shikari last updated on 29/Sep/20
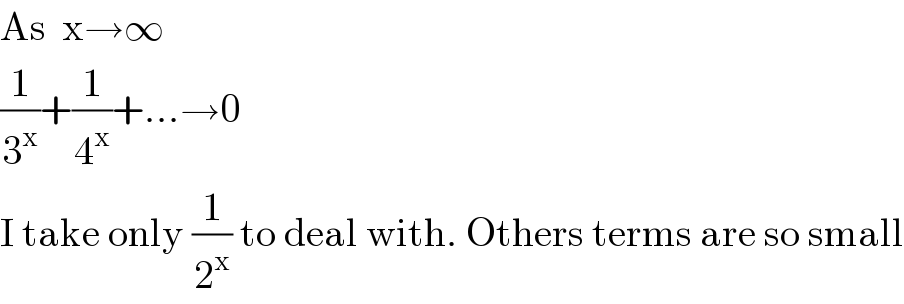
$$\mathrm{As}\:\:\mathrm{x}\rightarrow\infty \\ $$$$\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{x}} }+\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{x}} }+...\rightarrow\mathrm{0} \\ $$$$\mathrm{I}\:\mathrm{take}\:\mathrm{only}\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{x}} }\:\mathrm{to}\:\mathrm{deal}\:\mathrm{with}.\:\mathrm{Others}\:\mathrm{terms}\:\mathrm{are}\:\mathrm{so}\:\mathrm{small} \\ $$
Answered by Bird last updated on 29/Sep/20
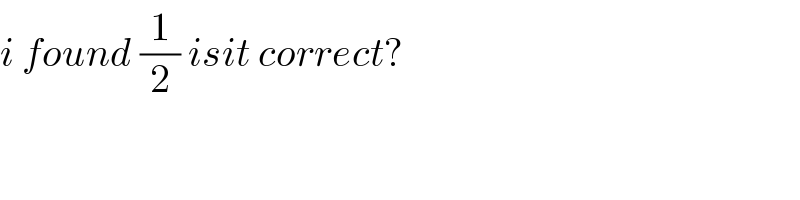
$${i}\:{found}\:\frac{\mathrm{1}}{\mathrm{2}}\:{isit}\:{correct}? \\ $$
Commented by mathdave last updated on 29/Sep/20

$${it}\:{is}\:{correct} \\ $$
Answered by Bird last updated on 29/Sep/20
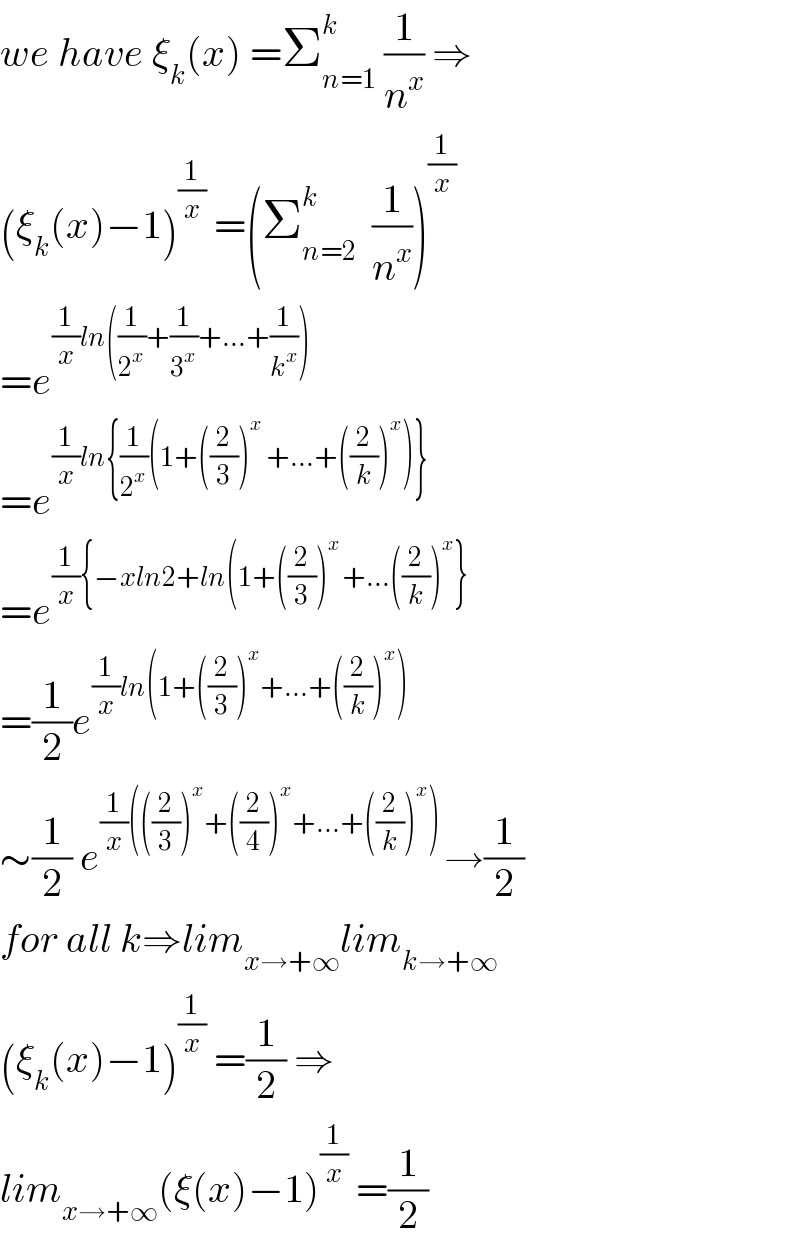
$${we}\:{have}\:\xi_{{k}} \left({x}\right)\:=\sum_{{n}=\mathrm{1}} ^{{k}} \:\frac{\mathrm{1}}{{n}^{{x}} }\:\Rightarrow \\ $$$$\left(\xi_{{k}} \left({x}\right)−\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}}} \:=\left(\sum_{{n}=\mathrm{2}} ^{{k}} \:\:\frac{\mathrm{1}}{{n}^{{x}} }\right)^{\frac{\mathrm{1}}{{x}}} \\ $$$$={e}^{\frac{\mathrm{1}}{{x}}{ln}\left(\frac{\mathrm{1}}{\mathrm{2}^{{x}} }+\frac{\mathrm{1}}{\mathrm{3}^{{x}} }+...+\frac{\mathrm{1}}{{k}^{{x}} }\right)} \\ $$$$={e}^{\frac{\mathrm{1}}{{x}}{ln}\left\{\frac{\mathrm{1}}{\mathrm{2}^{{x}} }\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} \:+...+\left(\frac{\mathrm{2}}{{k}}\right)^{{x}} \right)\right\}} \\ $$$$={e}^{\frac{\mathrm{1}}{{x}}\left\{−{xln}\mathrm{2}+{ln}\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}\:} +...\left(\frac{\mathrm{2}}{{k}}\right)^{{x}} \right\}\right.} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{e}^{\frac{\mathrm{1}}{{x}}{ln}\left(\mathrm{1}+\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} +...+\left(\frac{\mathrm{2}}{{k}}\right)^{{x}} \right)} \\ $$$$\sim\frac{\mathrm{1}}{\mathrm{2}}\:{e}^{\frac{\mathrm{1}}{{x}}\left(\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{x}} +\left(\frac{\mathrm{2}}{\mathrm{4}}\right)^{{x}} +...+\left(\frac{\mathrm{2}}{{k}}\right)^{{x}} \right)\:} \rightarrow\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${for}\:{all}\:{k}\Rightarrow{lim}_{{x}\rightarrow+\infty} {lim}_{{k}\rightarrow+\infty} \\ $$$$\left(\xi_{{k}} \left({x}\right)−\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}}} \:=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} \left(\xi\left({x}\right)−\mathrm{1}\right)^{\frac{\mathrm{1}}{{x}}} \:=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 30/Sep/20

$${nice}\:\:{very}\:{nice} \\ $$
