
Previous in Relation and Functions Next in Relation and Functions
Question Number 73047 by mathmax by abdo last updated on 05/Nov/19
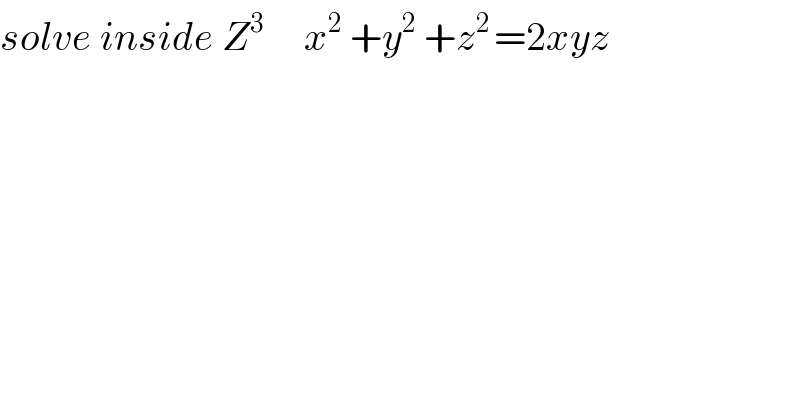
$${solve}\:{inside}\:{Z}^{\mathrm{3}} \:\:\:\:\:{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:+{z}^{\mathrm{2}\:} =\mathrm{2}{xyz} \\ $$
Answered by mind is power last updated on 07/Nov/19
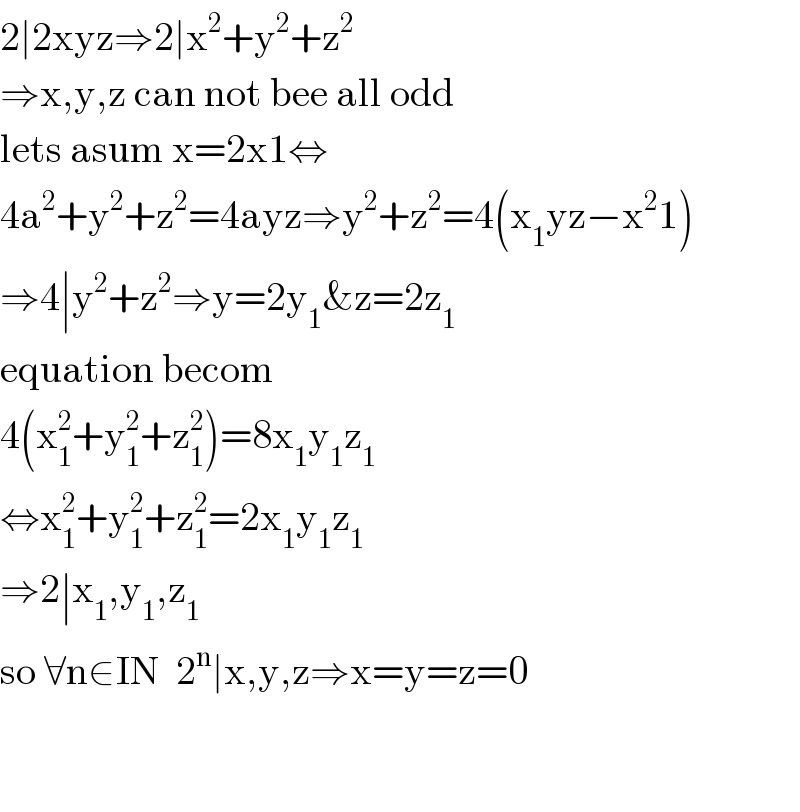
$$\mathrm{2}\mid\mathrm{2xyz}\Rightarrow\mathrm{2}\mid\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{x},\mathrm{y},\mathrm{z}\:\mathrm{can}\:\mathrm{not}\:\mathrm{bee}\:\mathrm{all}\:\mathrm{odd} \\ $$$$\mathrm{lets}\:\mathrm{asum}\:\mathrm{x}=\mathrm{2x1}\Leftrightarrow \\ $$$$\mathrm{4a}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{4ayz}\Rightarrow\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} =\mathrm{4}\left(\mathrm{x}_{\mathrm{1}} \mathrm{yz}−\mathrm{x}^{\mathrm{2}} \mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{4}\mid\mathrm{y}^{\mathrm{2}} +\mathrm{z}^{\mathrm{2}} \Rightarrow\mathrm{y}=\mathrm{2y}_{\mathrm{1}} \&\mathrm{z}=\mathrm{2z}_{\mathrm{1}} \\ $$$$\mathrm{equation}\:\mathrm{becom} \\ $$$$\mathrm{4}\left(\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{z}_{\mathrm{1}} ^{\mathrm{2}} \right)=\mathrm{8x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \mathrm{z}_{\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{x}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{y}_{\mathrm{1}} ^{\mathrm{2}} +\mathrm{z}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2x}_{\mathrm{1}} \mathrm{y}_{\mathrm{1}} \mathrm{z}_{\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2}\mid\mathrm{x}_{\mathrm{1}} ,\mathrm{y}_{\mathrm{1}} ,\mathrm{z}_{\mathrm{1}} \\ $$$$\mathrm{so}\:\forall\mathrm{n}\in\mathrm{IN}\:\:\mathrm{2}^{\mathrm{n}} \mid\mathrm{x},\mathrm{y},\mathrm{z}\Rightarrow\mathrm{x}=\mathrm{y}=\mathrm{z}=\mathrm{0} \\ $$$$ \\ $$$$ \\ $$
