
Question Number 42296 by maxmathsup by imad last updated on 22/Aug/18
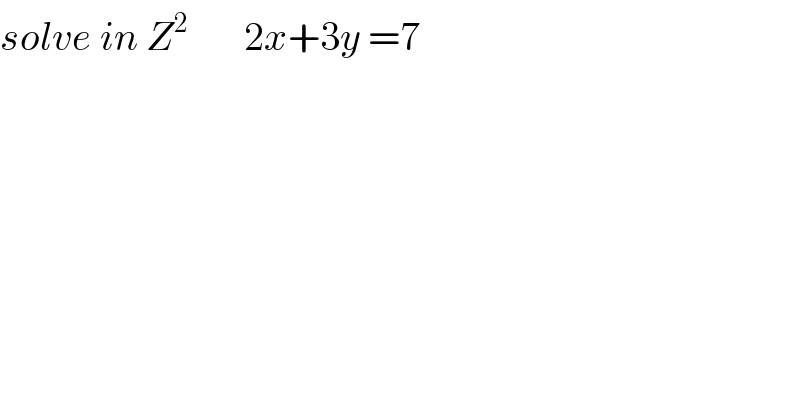
$${solve}\:{in}\:{Z}^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{2}{x}+\mathrm{3}{y}\:=\mathrm{7} \\ $$
Commented by math khazana by abdo last updated on 22/Aug/18
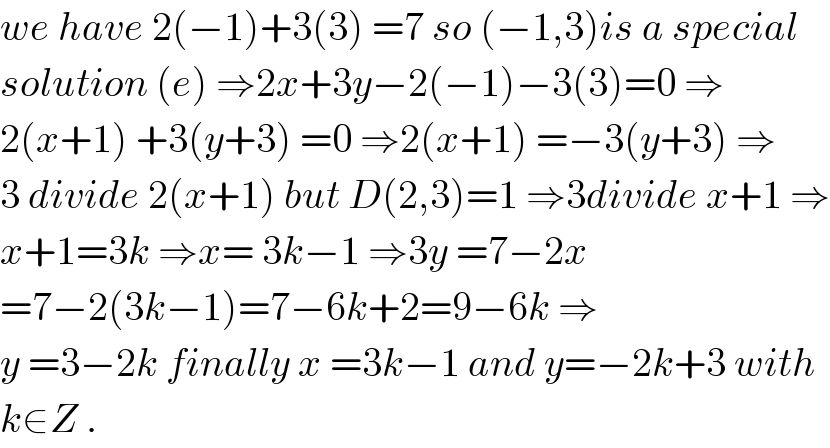
$${we}\:{have}\:\mathrm{2}\left(−\mathrm{1}\right)+\mathrm{3}\left(\mathrm{3}\right)\:=\mathrm{7}\:{so}\:\left(−\mathrm{1},\mathrm{3}\right){is}\:{a}\:{special} \\ $$$${solution}\:\left({e}\right)\:\Rightarrow\mathrm{2}{x}+\mathrm{3}{y}−\mathrm{2}\left(−\mathrm{1}\right)−\mathrm{3}\left(\mathrm{3}\right)=\mathrm{0}\:\Rightarrow \\ $$$$\mathrm{2}\left({x}+\mathrm{1}\right)\:+\mathrm{3}\left({y}+\mathrm{3}\right)\:=\mathrm{0}\:\Rightarrow\mathrm{2}\left({x}+\mathrm{1}\right)\:=−\mathrm{3}\left({y}+\mathrm{3}\right)\:\Rightarrow \\ $$$$\mathrm{3}\:{divide}\:\mathrm{2}\left({x}+\mathrm{1}\right)\:{but}\:{D}\left(\mathrm{2},\mathrm{3}\right)=\mathrm{1}\:\Rightarrow\mathrm{3}{divide}\:{x}+\mathrm{1}\:\Rightarrow \\ $$$${x}+\mathrm{1}=\mathrm{3}{k}\:\Rightarrow{x}=\:\mathrm{3}{k}−\mathrm{1}\:\Rightarrow\mathrm{3}{y}\:=\mathrm{7}−\mathrm{2}{x} \\ $$$$=\mathrm{7}−\mathrm{2}\left(\mathrm{3}{k}−\mathrm{1}\right)=\mathrm{7}−\mathrm{6}{k}+\mathrm{2}=\mathrm{9}−\mathrm{6}{k}\:\Rightarrow \\ $$$${y}\:=\mathrm{3}−\mathrm{2}{k}\:{finally}\:{x}\:=\mathrm{3}{k}−\mathrm{1}\:{and}\:{y}=−\mathrm{2}{k}+\mathrm{3}\:{with} \\ $$$${k}\in{Z}\:. \\ $$
Answered by ajfour last updated on 22/Aug/18
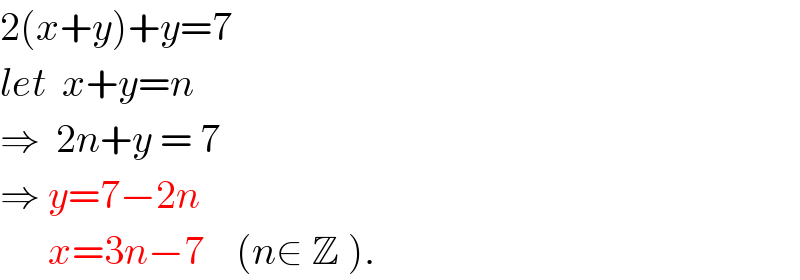
$$\mathrm{2}\left({x}+{y}\right)+{y}=\mathrm{7} \\ $$$${let}\:\:{x}+{y}={n} \\ $$$$\Rightarrow\:\:\mathrm{2}{n}+{y}\:=\:\mathrm{7} \\ $$$$\Rightarrow\:{y}=\mathrm{7}−\mathrm{2}{n} \\ $$$$\:\:\:\:\:\:{x}=\mathrm{3}{n}−\mathrm{7}\:\:\:\:\left({n}\in\:\mathbb{Z}\:\right). \\ $$
