
Question Number 169120 by mnjuly1970 last updated on 24/Apr/22
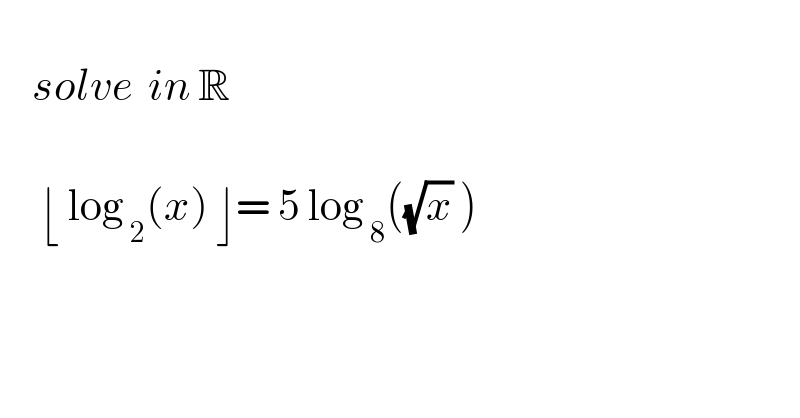
$$ \\ $$$$\:\:\:\:{solve}\:\:{in}\:\mathbb{R} \\ $$$$\: \\ $$$$\:\:\:\:\:\lfloor\:\mathrm{log}_{\:\mathrm{2}} \left({x}\right)\:\rfloor=\:\mathrm{5}\:\mathrm{log}_{\:\mathrm{8}} \left(\sqrt{{x}}\:\right) \\ $$$$ \\ $$
Answered by aleks041103 last updated on 24/Apr/22
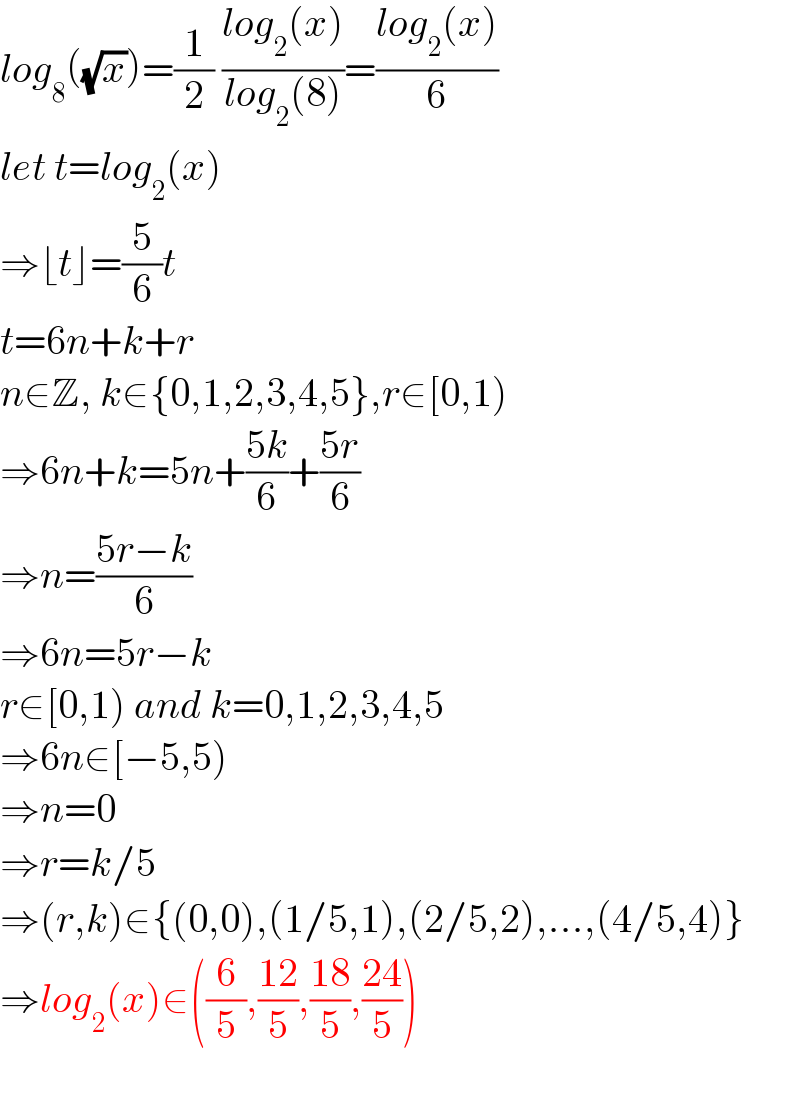
$${log}_{\mathrm{8}} \left(\sqrt{{x}}\right)=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{{log}_{\mathrm{2}} \left({x}\right)}{{log}_{\mathrm{2}} \left(\mathrm{8}\right)}=\frac{{log}_{\mathrm{2}} \left({x}\right)}{\mathrm{6}} \\ $$$${let}\:{t}={log}_{\mathrm{2}} \left({x}\right) \\ $$$$\Rightarrow\lfloor{t}\rfloor=\frac{\mathrm{5}}{\mathrm{6}}{t} \\ $$$${t}=\mathrm{6}{n}+{k}+{r} \\ $$$${n}\in\mathbb{Z},\:{k}\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5}\right\},{r}\in\left[\mathrm{0},\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{6}{n}+{k}=\mathrm{5}{n}+\frac{\mathrm{5}{k}}{\mathrm{6}}+\frac{\mathrm{5}{r}}{\mathrm{6}} \\ $$$$\Rightarrow{n}=\frac{\mathrm{5}{r}−{k}}{\mathrm{6}} \\ $$$$\Rightarrow\mathrm{6}{n}=\mathrm{5}{r}−{k} \\ $$$${r}\in\left[\mathrm{0},\mathrm{1}\right)\:{and}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4},\mathrm{5} \\ $$$$\Rightarrow\mathrm{6}{n}\in\left[−\mathrm{5},\mathrm{5}\right) \\ $$$$\Rightarrow{n}=\mathrm{0} \\ $$$$\Rightarrow{r}={k}/\mathrm{5} \\ $$$$\Rightarrow\left({r},{k}\right)\in\left\{\left(\mathrm{0},\mathrm{0}\right),\left(\mathrm{1}/\mathrm{5},\mathrm{1}\right),\left(\mathrm{2}/\mathrm{5},\mathrm{2}\right),...,\left(\mathrm{4}/\mathrm{5},\mathrm{4}\right)\right\} \\ $$$$\Rightarrow{log}_{\mathrm{2}} \left({x}\right)\in\left(\frac{\mathrm{6}}{\mathrm{5}},\frac{\mathrm{12}}{\mathrm{5}},\frac{\mathrm{18}}{\mathrm{5}},\frac{\mathrm{24}}{\mathrm{5}}\right) \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 25/Apr/22

$${thanks}\:{alot} \\ $$
Answered by floor(10²Eta[1]) last updated on 24/Apr/22
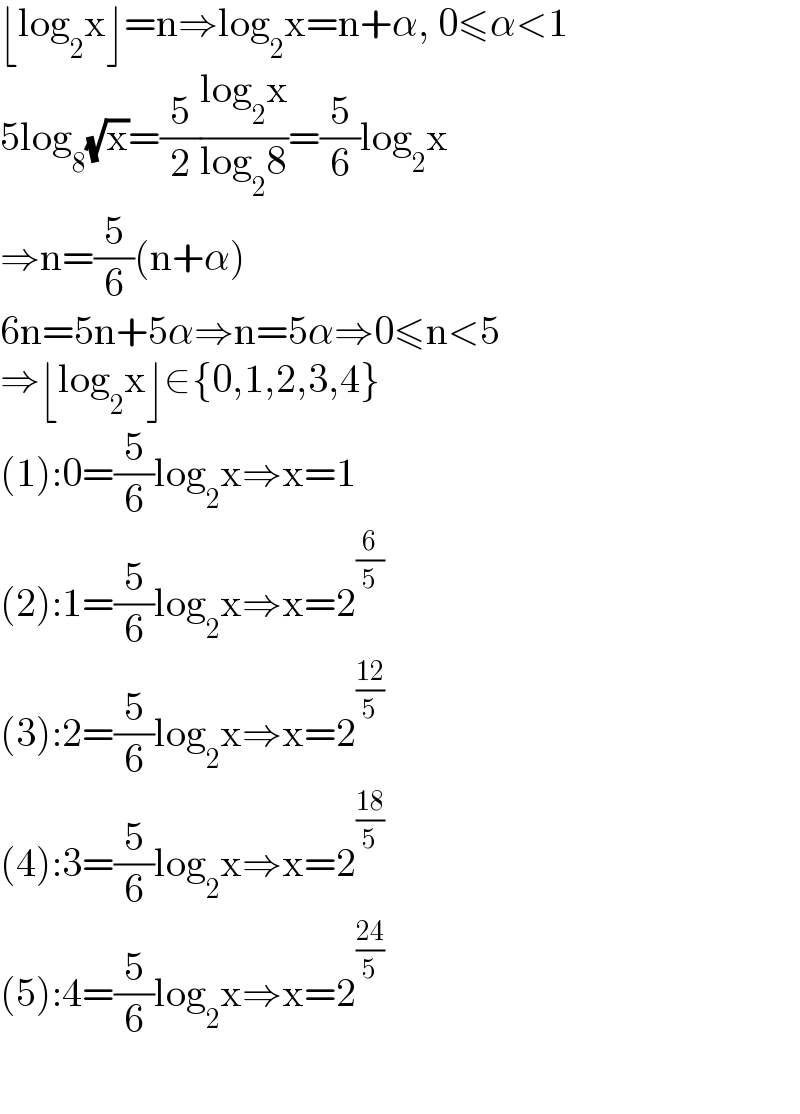
$$\lfloor\mathrm{log}_{\mathrm{2}} \mathrm{x}\rfloor=\mathrm{n}\Rightarrow\mathrm{log}_{\mathrm{2}} \mathrm{x}=\mathrm{n}+\alpha,\:\mathrm{0}\leqslant\alpha<\mathrm{1} \\ $$$$\mathrm{5log}_{\mathrm{8}} \sqrt{\mathrm{x}}=\frac{\mathrm{5}}{\mathrm{2}}\frac{\mathrm{log}_{\mathrm{2}} \mathrm{x}}{\mathrm{log}_{\mathrm{2}} \mathrm{8}}=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{log}_{\mathrm{2}} \mathrm{x} \\ $$$$\Rightarrow\mathrm{n}=\frac{\mathrm{5}}{\mathrm{6}}\left(\mathrm{n}+\alpha\right) \\ $$$$\mathrm{6n}=\mathrm{5n}+\mathrm{5}\alpha\Rightarrow\mathrm{n}=\mathrm{5}\alpha\Rightarrow\mathrm{0}\leqslant\mathrm{n}<\mathrm{5} \\ $$$$\Rightarrow\lfloor\mathrm{log}_{\mathrm{2}} \mathrm{x}\rfloor\in\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$$$\left(\mathrm{1}\right):\mathrm{0}=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{log}_{\mathrm{2}} \mathrm{x}\Rightarrow\mathrm{x}=\mathrm{1} \\ $$$$\left(\mathrm{2}\right):\mathrm{1}=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{log}_{\mathrm{2}} \mathrm{x}\Rightarrow\mathrm{x}=\mathrm{2}^{\frac{\mathrm{6}}{\mathrm{5}}} \\ $$$$\left(\mathrm{3}\right):\mathrm{2}=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{log}_{\mathrm{2}} \mathrm{x}\Rightarrow\mathrm{x}=\mathrm{2}^{\frac{\mathrm{12}}{\mathrm{5}}} \: \\ $$$$\left(\mathrm{4}\right):\mathrm{3}=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{log}_{\mathrm{2}} \mathrm{x}\Rightarrow\mathrm{x}=\mathrm{2}^{\frac{\mathrm{18}}{\mathrm{5}}} \\ $$$$\left(\mathrm{5}\right):\mathrm{4}=\frac{\mathrm{5}}{\mathrm{6}}\mathrm{log}_{\mathrm{2}} \mathrm{x}\Rightarrow\mathrm{x}=\mathrm{2}^{\frac{\mathrm{24}}{\mathrm{5}}} \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 25/Apr/22

$${grateful}\:... \\ $$
Answered by mahdipoor last updated on 24/Apr/22
![get x=2^t [log_2 x]=[t]=5log_8 ((√x))=((5×.5)/3)log_2 x=(5/6)t [t]=(5/6)t ⇒ t=(6/5)r , r∈Z ⇒ [(6/5)r]=r+[(r/5)]=r ⇒[(r/5)]=0 ⇒ r=0,1,2,3,4 ⇒x=2^t =2^((6/5)r) , r={0,1,2,3,4}](Q169133.png)
$${get}\:{x}=\mathrm{2}^{{t}} \\ $$$$\left[{log}_{\mathrm{2}} {x}\right]=\left[{t}\right]=\mathrm{5}{log}_{\mathrm{8}} \left(\sqrt{{x}}\right)=\frac{\mathrm{5}×.\mathrm{5}}{\mathrm{3}}{log}_{\mathrm{2}} {x}=\frac{\mathrm{5}}{\mathrm{6}}{t} \\ $$$$\left[{t}\right]=\frac{\mathrm{5}}{\mathrm{6}}{t}\:\:\:\:\Rightarrow\:\:\:{t}=\frac{\mathrm{6}}{\mathrm{5}}{r}\:\:\:,\:\:{r}\in\mathrm{Z}\:\Rightarrow \\ $$$$\left[\frac{\mathrm{6}}{\mathrm{5}}{r}\right]={r}+\left[\frac{{r}}{\mathrm{5}}\right]={r}\:\Rightarrow\left[\frac{{r}}{\mathrm{5}}\right]=\mathrm{0}\:\Rightarrow\:{r}=\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4} \\ $$$$\Rightarrow{x}=\mathrm{2}^{{t}} =\mathrm{2}^{\frac{\mathrm{6}}{\mathrm{5}}{r}} \:\:\:,\:\:{r}=\left\{\mathrm{0},\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}\right\} \\ $$
Commented by mnjuly1970 last updated on 25/Apr/22
$$\:\:\:{very}\:{nice}..{thx}\:{alot}... \\ $$
