
Question Number 168084 by mathocean1 last updated on 02/Apr/22
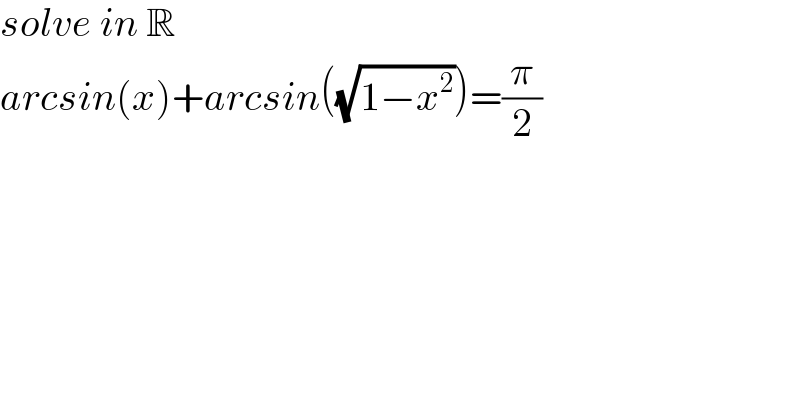
$${solve}\:{in}\:\mathbb{R} \\ $$$${arcsin}\left({x}\right)+{arcsin}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\frac{\pi}{\mathrm{2}} \\ $$
Commented by MJS_new last updated on 02/Apr/22

$${x}\geqslant\mathrm{0} \\ $$
Commented by mathocean1 last updated on 03/Apr/22
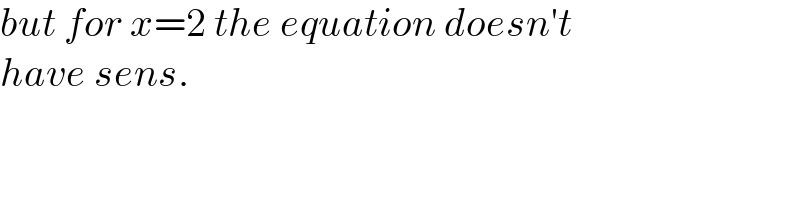
$${but}\:{for}\:{x}=\mathrm{2}\:{the}\:{equation}\:{doesn}'{t}\: \\ $$$${have}\:{sens}. \\ $$
Commented by MJS_new last updated on 03/Apr/22

$$\mathrm{arcsin}\:{a}\:+\mathrm{arcsin}\:{b}\:= \\ $$$$=\mathrm{arcsin}\:\left({a}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }+{b}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{with}\:{a}={x}\wedge{b}=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{arcsin}\:{x}\:+\mathrm{arcsin}\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:= \\ $$$$=\mathrm{arcsin}\:\left({x}\mid{x}\mid−{x}^{\mathrm{2}} +\mathrm{1}\right) \\ $$$$\mathrm{with}\:{x}<\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{arcsin}\:\left(\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \right) \\ $$$$\mathrm{with}\:{x}\geqslant\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:\mathrm{arcsin}\:\mathrm{1}\:=\frac{\pi}{\mathrm{2}} \\ $$$$\mathrm{doesn}'\mathrm{t}\:\mathrm{matter}\:\mathrm{if}\:\mathrm{arcsin}\:{x}\:\mathrm{and}\:\mathrm{arcsin}\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\mathrm{are}\:\mathrm{not}\:\mathrm{real},\:\mathrm{the}\:\mathrm{imaginary}\:\mathrm{part}\:\mathrm{vanishes} \\ $$$$\mathrm{arcsin}\:\mathrm{2}\:\approx\frac{\pi}{\mathrm{2}}−\mathrm{1}.\mathrm{31696i} \\ $$$$\mathrm{arcsin}\:\sqrt{\mathrm{1}−\mathrm{2}^{\mathrm{2}} }\:\approx\:\mathrm{1}.\mathrm{31696i} \\ $$
Answered by Tyller last updated on 04/Apr/22
![sen(arcsenx+arcsen((√(1−x^2 )))=1 x×(√(1−1+x^2 ))+(√(1−x^2 ))×(√(1−x^2 ))=1 x∣x∣+∣1−x^2 ∣=1 para x≥0 ∩ x∈[−1,1]⇒x∈[0,1] x×x+1−x^2 =1⇔x∈[0,1] para x<0 e (1−x^2 )≥0⇒x∈[−1,0) −x^2 +1−x^2 =1⇒x=0⇈ p/x≥0 e (1−x^2 )<0⇒x∈(−∝.−1)u(1.+∝) x^2 +x^2 −1=1⇒x=±1∉x sg=[0.1]](Q168137.png)
$${sen}\left({arcsenx}+{arcsen}\left(\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\mathrm{1}\right. \\ $$$${x}×\sqrt{\mathrm{1}−\mathrm{1}+{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }×\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }=\mathrm{1} \\ $$$${x}\mid{x}\mid+\mid\mathrm{1}−{x}^{\mathrm{2}} \mid=\mathrm{1} \\ $$$${para}\:{x}\geqslant\mathrm{0}\:\cap\:{x}\in\left[−\mathrm{1},\mathrm{1}\right]\Rightarrow{x}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$${x}×{x}+\mathrm{1}−{x}^{\mathrm{2}} =\mathrm{1}\Leftrightarrow{x}\in\left[\mathrm{0},\mathrm{1}\right] \\ $$$${para}\:{x}<\mathrm{0}\:{e}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)\geqslant\mathrm{0}\Rightarrow{x}\in\left[−\mathrm{1},\mathrm{0}\right) \\ $$$$−{x}^{\mathrm{2}} +\mathrm{1}−{x}^{\mathrm{2}} =\mathrm{1}\Rightarrow{x}=\mathrm{0}\upuparrows \\ $$$${p}/{x}\geqslant\mathrm{0}\:{e}\:\left(\mathrm{1}−{x}^{\mathrm{2}} \right)<\mathrm{0}\Rightarrow{x}\in\left(−\propto.−\mathrm{1}\right){u}\left(\mathrm{1}.+\propto\right) \\ $$$${x}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{1}\Rightarrow{x}=\pm\mathrm{1}\notin{x} \\ $$$${sg}=\left[\mathrm{0}.\mathrm{1}\right] \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Mathspace last updated on 04/Apr/22
![let ϕ(x)=arcsinx+arcsin(√(1−x^2 )) ϕ^′ (x)=(1/( (√(1−x^2 ))))−(x/( (√(1−x^2 ))))×(1/( (√(1−(1−x^2 ))))) =(1/( (√(1−x^2 ))))(1−(x/( (√x^2 )))) =(1/( (√(1−x^2 ))))(1−(x/(∣x∣))) so if x∈]0,1[ we get ϕ^′ (x)=0 ⇒](Q168152.png)
$${let}\:\varphi\left({x}\right)={arcsinx}+{arcsin}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\varphi^{'} \left({x}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}−\frac{{x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}×\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left(\mathrm{1}−\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} }}\right) \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\left(\mathrm{1}−\frac{{x}}{\mid{x}\mid}\right) \\ $$$$\left.{so}\:{if}\:{x}\in\right]\mathrm{0},\mathrm{1}\left[\:\:{we}\:{get}\:\varphi^{'} \left({x}\right)=\mathrm{0}\:\Rightarrow\right. \\ $$$$ \\ $$
Answered by Mathspace last updated on 04/Apr/22
![⇒ϕ(x)=C x=0 ⇒o+arcsin(1)=C ⇒ C=(π/2) ⇒set of solution is [0,1]](Q168153.png)
$$\Rightarrow\varphi\left({x}\right)={C} \\ $$$${x}=\mathrm{0}\:\Rightarrow{o}+{arcsin}\left(\mathrm{1}\right)={C}\:\Rightarrow \\ $$$${C}=\frac{\pi}{\mathrm{2}}\:\Rightarrow{set}\:{of}\:{solution}\:{is}\:\left[\mathrm{0},\mathrm{1}\right] \\ $$
Commented by MJS_new last updated on 04/Apr/22
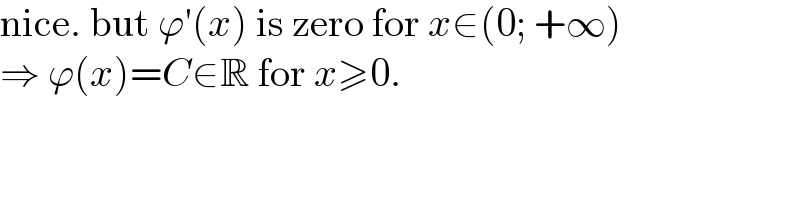
$$\mathrm{nice}.\:\mathrm{but}\:\varphi'\left({x}\right)\:\mathrm{is}\:\mathrm{zero}\:\mathrm{for}\:{x}\in\left(\mathrm{0};\:+\infty\right) \\ $$$$\Rightarrow\:\varphi\left({x}\right)={C}\in\mathbb{R}\:\mathrm{for}\:{x}\geqslant\mathrm{0}.\: \\ $$
