
Question Number 104588 by M±th+et+s last updated on 22/Jul/20
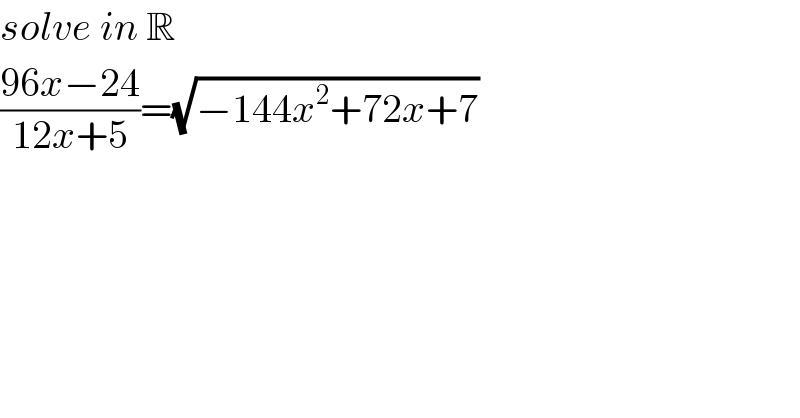
$${solve}\:{in}\:\mathbb{R} \\ $$$$\frac{\mathrm{96}{x}−\mathrm{24}}{\mathrm{12}{x}+\mathrm{5}}=\sqrt{−\mathrm{144}{x}^{\mathrm{2}} +\mathrm{72}{x}+\mathrm{7}} \\ $$
Commented by M±th+et+s last updated on 22/Jul/20
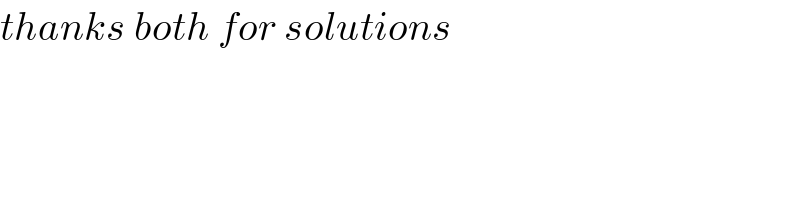
$${thanks}\:{both}\:{for}\:{solutions} \\ $$
Answered by ajfour last updated on 22/Jul/20
![8−(((64)/(12x+5)))=(√(16−(12x−3)^2 )) let 12x−3=t with −4≤t≤4 ⇒ 8−((64)/(t+8))=(√(16−t^2 )) ⇒ 4−(√(16−t^2 ))=((64)/(t+8))−4 ....(i) ⇒ (t^2 /(4+(√(16−t^2 )))) = ((64)/(t+8))−4 ⇒ 4+(√(16−t^2 )) = (t^2 /4)(((t+8)/(8−t))) ...(ii) Adding (i) & (ii) 8=(t^2 /4)(((t+8)/(8−t)))+4(((8−t)/(t+8))) Now let ((8−t)/(t+8)) = s ⇒ t=8(((1−s)/(s+1))) ⇒ 8=16(((1−s)/(s+1)))^2 ((1/s))+4s ⇒ 2s(s+1)^2 =4(1−s)^2 +s^2 (s+1)^2 ⇒ s(s+1)^2 (2−s)=4(1−s)^2 ⇒ (s+1)^2 [1−(s−1)^2 ]=4(1−s)^2 ⇒ (1/((1−s)^2 ))−(4/((1+s)^2 )) = 1 ......](Q104596.png)
$$\mathrm{8}−\left(\frac{\mathrm{64}}{\mathrm{12}{x}+\mathrm{5}}\right)=\sqrt{\mathrm{16}−\left(\mathrm{12}{x}−\mathrm{3}\right)^{\mathrm{2}} } \\ $$$${let}\:\:\mathrm{12}{x}−\mathrm{3}={t}\:\:\:{with}\:\:\:−\mathrm{4}\leqslant{t}\leqslant\mathrm{4} \\ $$$$\Rightarrow\:\:\mathrm{8}−\frac{\mathrm{64}}{{t}+\mathrm{8}}=\sqrt{\mathrm{16}−{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\mathrm{4}−\sqrt{\mathrm{16}−{t}^{\mathrm{2}} }=\frac{\mathrm{64}}{{t}+\mathrm{8}}−\mathrm{4}\:\:\:\:\:....\left({i}\right) \\ $$$$\Rightarrow\:\:\:\frac{{t}^{\mathrm{2}} }{\mathrm{4}+\sqrt{\mathrm{16}−{t}^{\mathrm{2}} }}\:=\:\frac{\mathrm{64}}{{t}+\mathrm{8}}−\mathrm{4} \\ $$$$\Rightarrow\:\:\mathrm{4}+\sqrt{\mathrm{16}−{t}^{\mathrm{2}} }\:=\:\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{{t}+\mathrm{8}}{\mathrm{8}−{t}}\right)\:\:\:...\left({ii}\right) \\ $$$${Adding}\:\:\left({i}\right)\:\&\:\left({ii}\right) \\ $$$$\:\:\:\:\:\mathrm{8}=\frac{{t}^{\mathrm{2}} }{\mathrm{4}}\left(\frac{{t}+\mathrm{8}}{\mathrm{8}−{t}}\right)+\mathrm{4}\left(\frac{\mathrm{8}−{t}}{{t}+\mathrm{8}}\right) \\ $$$${Now}\:{let}\:\:\frac{\mathrm{8}−{t}}{{t}+\mathrm{8}}\:=\:{s}\:\:\Rightarrow\:\:{t}=\mathrm{8}\left(\frac{\mathrm{1}−{s}}{{s}+\mathrm{1}}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{8}=\mathrm{16}\left(\frac{\mathrm{1}−{s}}{{s}+\mathrm{1}}\right)^{\mathrm{2}} \:\:\left(\frac{\mathrm{1}}{{s}}\right)+\mathrm{4}{s} \\ $$$$\Rightarrow\:\:\:\:\mathrm{2}{s}\left({s}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\left(\mathrm{1}−{s}\right)^{\mathrm{2}} +{s}^{\mathrm{2}} \left({s}+\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:{s}\left({s}+\mathrm{1}\right)^{\mathrm{2}} \left(\mathrm{2}−{s}\right)=\mathrm{4}\left(\mathrm{1}−{s}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\left({s}+\mathrm{1}\right)^{\mathrm{2}} \left[\mathrm{1}−\left({s}−\mathrm{1}\right)^{\mathrm{2}} \right]=\mathrm{4}\left(\mathrm{1}−{s}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\frac{\mathrm{1}}{\left(\mathrm{1}−{s}\right)^{\mathrm{2}} }−\frac{\mathrm{4}}{\left(\mathrm{1}+{s}\right)^{\mathrm{2}} }\:=\:\mathrm{1} \\ $$$$...... \\ $$
