
Question Number 191343 by mnjuly1970 last updated on 23/Apr/23

$$ \\ $$$$\:\:\:\:\:\:\mathrm{solve}\:\:{in}\:\:\mathbb{R} \\ $$$$ \\ $$$$\:\:\:\:\:\:\lfloor\:\frac{\mathrm{1}}{{x}}\:\rfloor\:+\:\lfloor\:\frac{\mathrm{2}}{{x}}\:\rfloor\:+\:\lfloor\:\frac{\mathrm{3}}{{x}}\:\rfloor\:=\:\mathrm{1} \\ $$$$ \\ $$
Answered by mr W last updated on 23/Apr/23
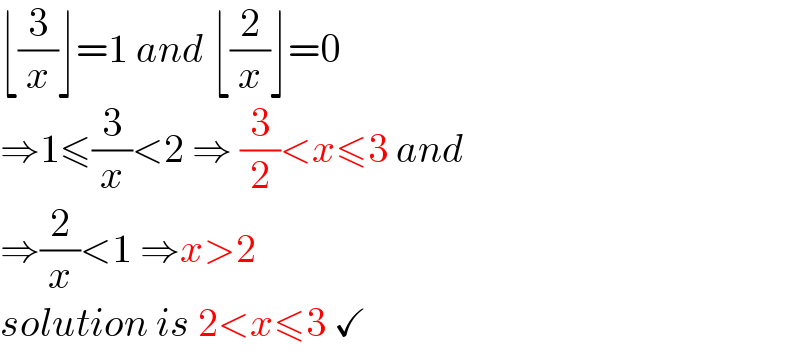
$$\lfloor\frac{\mathrm{3}}{{x}}\rfloor=\mathrm{1}\:{and}\:\lfloor\frac{\mathrm{2}}{{x}}\rfloor=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}\leqslant\frac{\mathrm{3}}{{x}}<\mathrm{2}\:\Rightarrow\:\frac{\mathrm{3}}{\mathrm{2}}<{x}\leqslant\mathrm{3}\:{and} \\ $$$$\Rightarrow\frac{\mathrm{2}}{{x}}<\mathrm{1}\:\Rightarrow{x}>\mathrm{2} \\ $$$${solution}\:{is}\:\mathrm{2}<{x}\leqslant\mathrm{3}\:\checkmark \\ $$
Commented by mnjuly1970 last updated on 23/Apr/23
$$\:\:{thank}\:{you}\:{so}\:{much}\:{sir}\:{W}\: \\ $$
