
Question Number 187963 by Humble last updated on 24/Feb/23
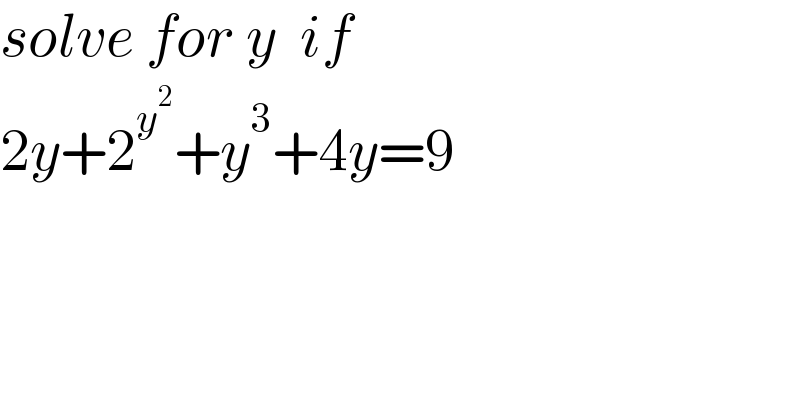
$${solve}\:{for}\:{y}\:\:{if} \\ $$$$\mathrm{2}{y}+\mathrm{2}^{{y}^{\mathrm{2}} } +{y}^{\mathrm{3}} +\mathrm{4}{y}=\mathrm{9} \\ $$
Answered by a.lgnaoui last updated on 24/Feb/23
![6y+2^y^2 +y^3 =9 y(y^2 +6)+2^y^2 =9 y^2 +6+(2^y^2 /y)=(9/y) y^2 +6=(1/y)(9−2^y^2 )⇒ (y^2 +6)^2 =(1/y^2 )(9−2^y^2 )^2 z=y^2 (z+6+((9−2^z )/z))(z+6−((9−2^z )/z))=0 ⇒ (z+3)^2 −2^z =0 (1) z^2 +6z−9+2^z =0 (2) (1)+(2)⇒ (z+3)^2 +z^2 +6z−9=0 2z(z+6)=0 { (((z+3)^2 =2^z )),(((z+3)^2 −18+2^z =0)) :} (suite) (z+3)^2 =2^z zlog2=2log(z+3) [(z+3) −3]log2 =log(z+3) z+3=t (t−3)log2=logt tlog2−logt=3log2 log((2^t /t) )=log(2^3 ) (2^t /t)=2^3 (2^(y^2 +3) /(y^2 +3))=2^3 =2^3 (2^y^2 /(y^2 +3)) (2^y^2 /(y^2 +3))=1⇒2^y^2 =y^2 +3 Solution={−1;+1}](Q188022.png)
$$\mathrm{6}{y}+\mathrm{2}^{{y}^{\mathrm{2}} } +{y}^{\mathrm{3}} =\mathrm{9} \\ $$$${y}\left({y}^{\mathrm{2}} +\mathrm{6}\right)+\mathrm{2}^{{y}^{\mathrm{2}} } =\mathrm{9} \\ $$$${y}^{\mathrm{2}} +\mathrm{6}+\frac{\mathrm{2}^{{y}^{\mathrm{2}} } }{{y}}=\frac{\mathrm{9}}{{y}} \\ $$$${y}^{\mathrm{2}} +\mathrm{6}=\frac{\mathrm{1}}{{y}}\left(\mathrm{9}−\mathrm{2}^{{y}^{\mathrm{2}} } \right)\Rightarrow \\ $$$$\left({y}^{\mathrm{2}} +\mathrm{6}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\left(\mathrm{9}−\mathrm{2}^{{y}^{\mathrm{2}} } \right)^{\mathrm{2}} \\ $$$${z}={y}^{\mathrm{2}} \\ $$$$\:\:\:\left({z}+\mathrm{6}+\frac{\mathrm{9}−\mathrm{2}^{{z}} }{{z}}\right)\left({z}+\mathrm{6}−\frac{\mathrm{9}−\mathrm{2}^{{z}} }{{z}}\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\left({z}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{2}^{{z}} \:\:\:\:=\mathrm{0}\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$${z}^{\mathrm{2}} +\mathrm{6}{z}−\mathrm{9}+\mathrm{2}^{{z}} =\mathrm{0}\:\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\Rightarrow \\ $$$$\left({z}+\mathrm{3}\right)^{\mathrm{2}} +{z}^{\mathrm{2}} +\mathrm{6}{z}−\mathrm{9}=\mathrm{0} \\ $$$$\mathrm{2}{z}\left({z}+\mathrm{6}\right)=\mathrm{0}\:\:\:\:\:\:\: \\ $$$$\begin{cases}{\left({z}+\mathrm{3}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{{z}} }\\{\left({z}+\mathrm{3}\right)^{\mathrm{2}} −\mathrm{18}+\mathrm{2}^{{z}} =\mathrm{0}}\end{cases} \\ $$$$\:\:\:\:\left({suite}\right) \\ $$$$ \\ $$$$\left({z}+\mathrm{3}\right)^{\mathrm{2}} =\mathrm{2}^{{z}} \:\: \\ $$$${z}\mathrm{log2}=\mathrm{2log}\left(\mathrm{z}+\mathrm{3}\right) \\ $$$$\left[\left(\mathrm{z}+\mathrm{3}\right)\:−\mathrm{3}\right]\mathrm{log2}\:=\mathrm{log}\left(\mathrm{z}+\mathrm{3}\right) \\ $$$$\mathrm{z}+\mathrm{3}=\mathrm{t} \\ $$$$\left(\mathrm{t}−\mathrm{3}\right)\mathrm{log2}=\mathrm{logt} \\ $$$$\mathrm{tlog2}−\mathrm{logt}=\mathrm{3log2} \\ $$$$\mathrm{log}\left(\frac{\mathrm{2}^{\mathrm{t}} }{\mathrm{t}}\:\right)=\mathrm{log}\left(\mathrm{2}^{\mathrm{3}} \right) \\ $$$$\:\:\:\:\:\:\frac{\mathrm{2}^{\mathrm{t}} }{\mathrm{t}}=\mathrm{2}^{\mathrm{3}} \:\: \\ $$$$\:\:\:\:\:\frac{\mathrm{2}^{{y}^{\mathrm{2}} +\mathrm{3}} }{{y}^{\mathrm{2}} +\mathrm{3}}=\mathrm{2}^{\mathrm{3}} =\mathrm{2}^{\mathrm{3}} \frac{\mathrm{2}^{{y}^{\mathrm{2}} } }{{y}^{\mathrm{2}} +\mathrm{3}} \\ $$$$\:\:\:\:\frac{\mathrm{2}^{{y}^{\mathrm{2}} } }{{y}^{\mathrm{2}} +\mathrm{3}}=\mathrm{1}\Rightarrow\mathrm{2}^{{y}^{\mathrm{2}} } ={y}^{\mathrm{2}} +\mathrm{3} \\ $$$$\:\:\:\:\:\:\: \\ $$$$\boldsymbol{{Solution}}=\left\{−\mathrm{1};+\mathrm{1}\right\} \\ $$$$\:\:\: \\ $$
Commented by Humble last updated on 25/Feb/23
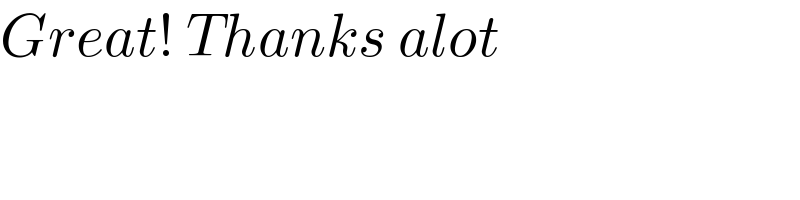
$${Great}!\:{Thanks}\:{alot} \\ $$
Commented by mr W last updated on 25/Feb/23
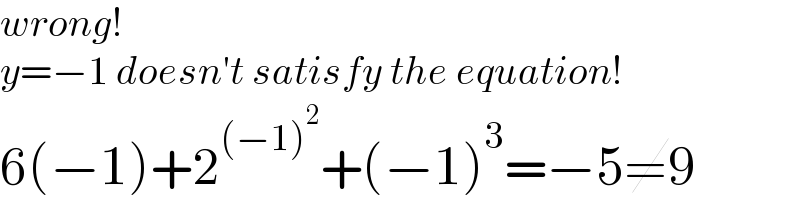
$${wrong}! \\ $$$${y}=−\mathrm{1}\:{doesn}'{t}\:{satisfy}\:{the}\:{equation}! \\ $$$$\mathrm{6}\left(−\mathrm{1}\right)+\mathrm{2}^{\left(−\mathrm{1}\right)^{\mathrm{2}} } +\left(−\mathrm{1}\right)^{\mathrm{3}} =−\mathrm{5}\neq\mathrm{9} \\ $$
