
Question Number 49188 by behi83417@gmail.com last updated on 04/Dec/18
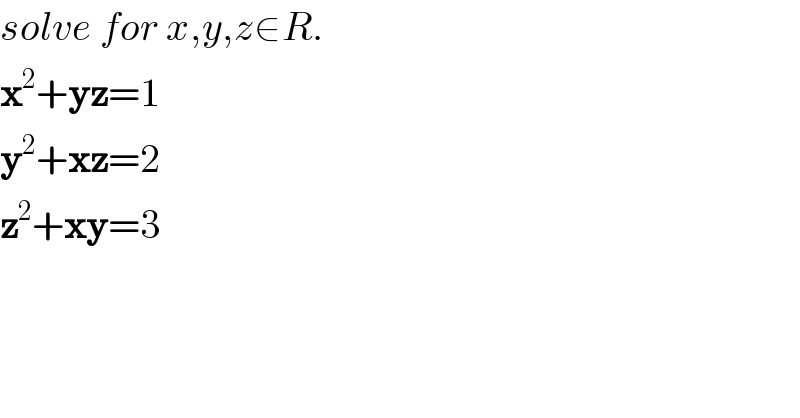
$${solve}\:{for}\:{x},{y},{z}\in{R}. \\ $$$$\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{yz}}=\mathrm{1} \\ $$$$\boldsymbol{\mathrm{y}}^{\mathrm{2}} +\boldsymbol{\mathrm{xz}}=\mathrm{2} \\ $$$$\boldsymbol{\mathrm{z}}^{\mathrm{2}} +\boldsymbol{\mathrm{xy}}=\mathrm{3} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 05/Dec/18
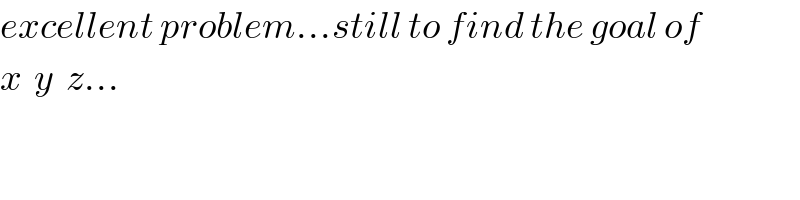
$${excellent}\:{problem}...{still}\:{to}\:{find}\:{the}\:{goal}\:{of} \\ $$$${x}\:\:{y}\:\:{z}... \\ $$
Answered by ajfour last updated on 04/Dec/18
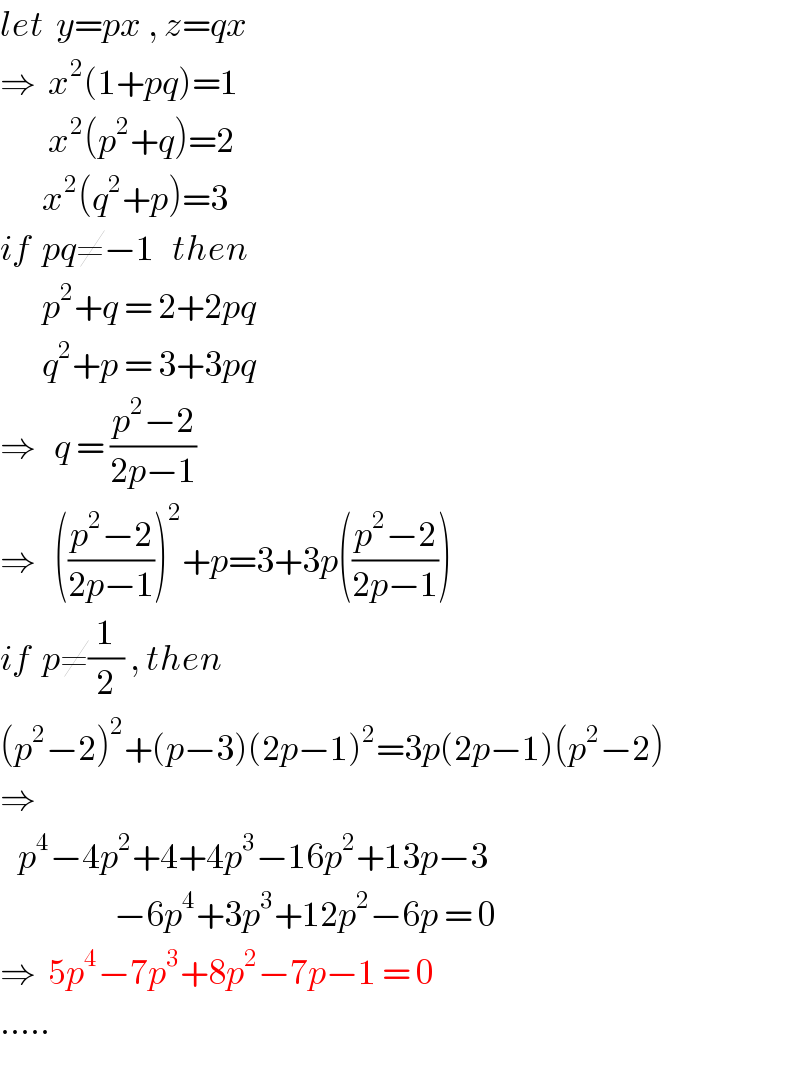
$${let}\:\:{y}={px}\:,\:{z}={qx} \\ $$$$\Rightarrow\:\:{x}^{\mathrm{2}} \left(\mathrm{1}+{pq}\right)=\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} \left({p}^{\mathrm{2}} +{q}\right)=\mathrm{2} \\ $$$$\:\:\:\:\:\:\:{x}^{\mathrm{2}} \left({q}^{\mathrm{2}} +{p}\right)=\mathrm{3} \\ $$$${if}\:\:{pq}\neq−\mathrm{1}\:\:\:{then} \\ $$$$\:\:\:\:\:\:\:{p}^{\mathrm{2}} +{q}\:=\:\mathrm{2}+\mathrm{2}{pq} \\ $$$$\:\:\:\:\:\:\:{q}^{\mathrm{2}} +{p}\:=\:\mathrm{3}+\mathrm{3}{pq} \\ $$$$\Rightarrow\:\:\:{q}\:=\:\frac{{p}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{p}−\mathrm{1}} \\ $$$$\Rightarrow\:\:\:\left(\frac{{p}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{p}−\mathrm{1}}\right)^{\mathrm{2}} +{p}=\mathrm{3}+\mathrm{3}{p}\left(\frac{{p}^{\mathrm{2}} −\mathrm{2}}{\mathrm{2}{p}−\mathrm{1}}\right) \\ $$$${if}\:\:{p}\neq\frac{\mathrm{1}}{\mathrm{2}}\:,\:{then} \\ $$$$\left({p}^{\mathrm{2}} −\mathrm{2}\right)^{\mathrm{2}} +\left({p}−\mathrm{3}\right)\left(\mathrm{2}{p}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{3}{p}\left(\mathrm{2}{p}−\mathrm{1}\right)\left({p}^{\mathrm{2}} −\mathrm{2}\right) \\ $$$$\Rightarrow \\ $$$$\:\:\:{p}^{\mathrm{4}} −\mathrm{4}{p}^{\mathrm{2}} +\mathrm{4}+\mathrm{4}{p}^{\mathrm{3}} −\mathrm{16}{p}^{\mathrm{2}} +\mathrm{13}{p}−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{6}{p}^{\mathrm{4}} +\mathrm{3}{p}^{\mathrm{3}} +\mathrm{12}{p}^{\mathrm{2}} −\mathrm{6}{p}\:=\:\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{5}{p}^{\mathrm{4}} −\mathrm{7}{p}^{\mathrm{3}} +\mathrm{8}{p}^{\mathrm{2}} −\mathrm{7}{p}−\mathrm{1}\:=\:\mathrm{0} \\ $$$$..... \\ $$
