
Question Number 206922 by mr W last updated on 01/May/24
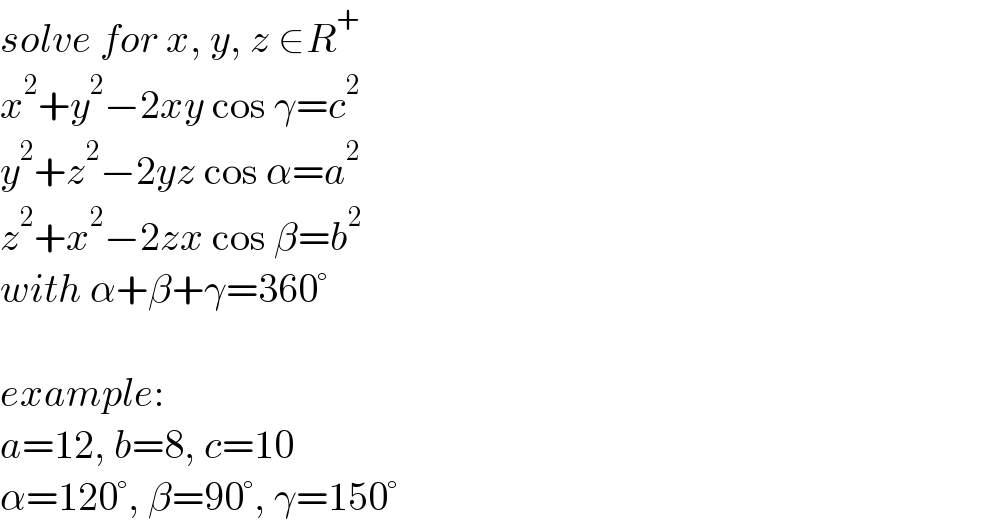
$${solve}\:{for}\:{x},\:{y},\:{z}\:\in{R}^{+} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} −\mathrm{2}{xy}\:\mathrm{cos}\:\gamma={c}^{\mathrm{2}} \\ $$$${y}^{\mathrm{2}} +{z}^{\mathrm{2}} −\mathrm{2}{yz}\:\mathrm{cos}\:\alpha={a}^{\mathrm{2}} \\ $$$${z}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}{zx}\:\mathrm{cos}\:\beta={b}^{\mathrm{2}} \\ $$$${with}\:\alpha+\beta+\gamma=\mathrm{360}° \\ $$$$ \\ $$$${example}:\: \\ $$$${a}=\mathrm{12},\:{b}=\mathrm{8},\:{c}=\mathrm{10} \\ $$$$\alpha=\mathrm{120}°,\:\beta=\mathrm{90}°,\:\gamma=\mathrm{150}° \\ $$
Answered by mr W last updated on 01/May/24
Commented by mr W last updated on 01/May/24
Commented by mr W last updated on 01/May/24
![∠A=cos^(−1) ((b^2 +c^2 −a^2 )/(2bc)) ∠B=cos^(−1) ((c^2 +a^2 −b^2 )/(2ca)) ∠C=cos^(−1) ((a^2 +b^2 −c^2 )/(2ab)) π−2φ_1 =2π−2α ⇒φ_1 =α−(π/2) similarly φ_2 =β−(π/2) φ_3 =γ−(π/2) r_1 =(a/(2 cos φ_1 ))=(a/(2 sin α)) similarly r_2 =(b/(2 sin β)) r_3 =(c/(2 sin γ)) QR^2 =r_2 ^2 +r_3 ^2 −2r_2 r_3 cos (∠A+φ_2 +φ_3 ) ∠A+φ_2 +φ_3 =∠A+β+γ−π=π−(α−∠A) QR^2 =(b^2 /(4 sin^2 β))+(c^2 /(4 sin^2 γ))+((bc cos (α−∠A) )/(2 sin β sin γ)) ((x×QR)/2)=r_2 r_3 sin (∠A+φ_2 +φ_3 )=2[AQR] ((x×QR)/2)=((bc sin (α−∠A))/(4 sin β sin γ)) ⇒x=((bc sin (α−∠A))/(sin β sin γ (√((b^2 /(sin^2 β))+(c^2 /(sin^2 γ))+((2bc cos (α−∠A) )/(sin β sin γ)))))) similarly ⇒y=((ca sin (β−∠B))/(sin γ sin α (√((c^2 /(sin^2 γ))+(a^2 /(sin^2 α))+((2ca cos (β−∠B) )/(sin γ sin a)))))) ⇒z=((ab sin (γ−∠C))/(sin α sin β (√((a^2 /(sin^2 α))+(b^2 /(sin^2 β))+((2ab cos (γ−∠C) )/(sin α sin β)))))) example: a=12, b=8, c=10 α=120°, β=90°, γ=150° cos ∠C=((12^2 +8^2 −10^2 )/(2×12×8))=(9/(16)) sin (γ−∠C)=((9+5(√(21)))/(32)) cos (γ−∠C)=((−9(√3)+5(√7))/(32)) z=((12×8×((9+5(√(21)))/(32)))/(((√3)/2) (√(((12^2 ×4)/3)+8^2 +((2×12×8×2 )/( (√3)))×((−9(√3)+5(√7))/(32)))))) =((9(√3)+15(√7))/( (√(37+5(√(21))))))≈7.141](Q206929.png)
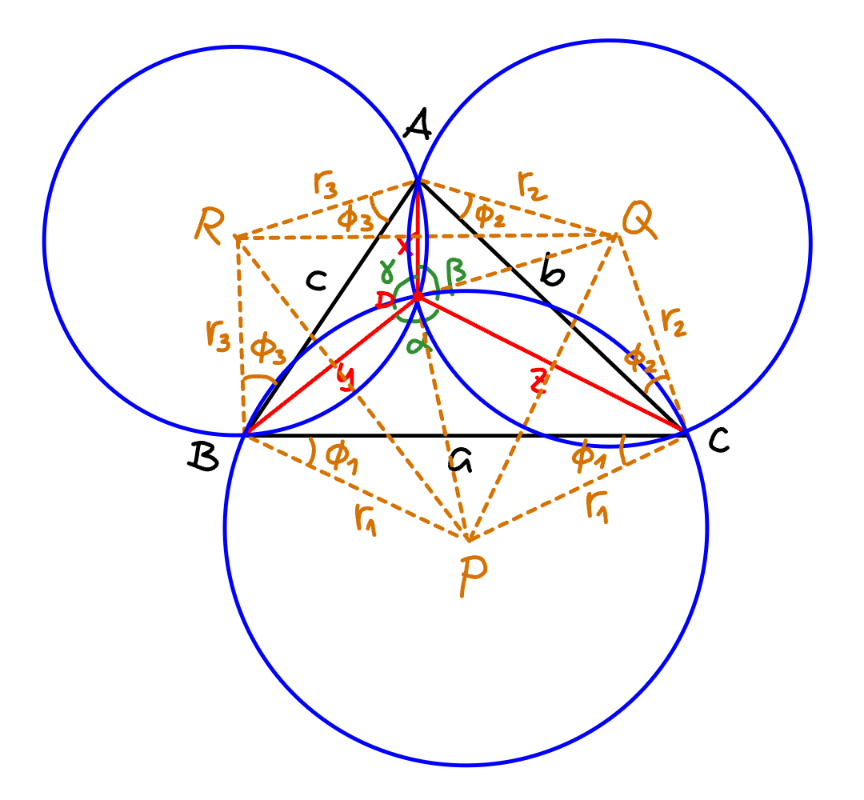
$$\angle{A}=\mathrm{cos}^{−\mathrm{1}} \frac{{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −{a}^{\mathrm{2}} }{\mathrm{2}{bc}} \\ $$$$\angle{B}=\mathrm{cos}^{−\mathrm{1}} \frac{{c}^{\mathrm{2}} +{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }{\mathrm{2}{ca}} \\ $$$$\angle{C}=\mathrm{cos}^{−\mathrm{1}} \frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −{c}^{\mathrm{2}} }{\mathrm{2}{ab}} \\ $$$$\pi−\mathrm{2}\phi_{\mathrm{1}} =\mathrm{2}\pi−\mathrm{2}\alpha\: \\ $$$$\Rightarrow\phi_{\mathrm{1}} =\alpha−\frac{\pi}{\mathrm{2}} \\ $$$${similarly} \\ $$$$\phi_{\mathrm{2}} =\beta−\frac{\pi}{\mathrm{2}} \\ $$$$\phi_{\mathrm{3}} =\gamma−\frac{\pi}{\mathrm{2}} \\ $$$${r}_{\mathrm{1}} =\frac{{a}}{\mathrm{2}\:\mathrm{cos}\:\phi_{\mathrm{1}} }=\frac{{a}}{\mathrm{2}\:\mathrm{sin}\:\alpha} \\ $$$${similarly} \\ $$$${r}_{\mathrm{2}} =\frac{{b}}{\mathrm{2}\:\mathrm{sin}\:\beta} \\ $$$${r}_{\mathrm{3}} =\frac{{c}}{\mathrm{2}\:\mathrm{sin}\:\gamma} \\ $$$${QR}^{\mathrm{2}} ={r}_{\mathrm{2}} ^{\mathrm{2}} +{r}_{\mathrm{3}} ^{\mathrm{2}} −\mathrm{2}{r}_{\mathrm{2}} {r}_{\mathrm{3}} \:\mathrm{cos}\:\left(\angle{A}+\phi_{\mathrm{2}} +\phi_{\mathrm{3}} \right) \\ $$$$\angle{A}+\phi_{\mathrm{2}} +\phi_{\mathrm{3}} =\angle{A}+\beta+\gamma−\pi=\pi−\left(\alpha−\angle{A}\right) \\ $$$${QR}^{\mathrm{2}} =\frac{{b}^{\mathrm{2}} }{\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta}+\frac{{c}^{\mathrm{2}} }{\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\gamma}+\frac{{bc}\:\mathrm{cos}\:\left(\alpha−\angle{A}\right)\:}{\mathrm{2}\:\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma} \\ $$$$\frac{{x}×{QR}}{\mathrm{2}}={r}_{\mathrm{2}} {r}_{\mathrm{3}} \:\mathrm{sin}\:\left(\angle{A}+\phi_{\mathrm{2}} +\phi_{\mathrm{3}} \right)=\mathrm{2}\left[{AQR}\right] \\ $$$$\frac{{x}×{QR}}{\mathrm{2}}=\frac{{bc}\:\mathrm{sin}\:\left(\alpha−\angle{A}\right)}{\mathrm{4}\:\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma} \\ $$$$\Rightarrow{x}=\frac{{bc}\:\mathrm{sin}\:\left(\alpha−\angle{A}\right)}{\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma\:\sqrt{\frac{{b}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\beta}+\frac{{c}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\gamma}+\frac{\mathrm{2}{bc}\:\mathrm{cos}\:\left(\alpha−\angle{A}\right)\:}{\mathrm{sin}\:\beta\:\mathrm{sin}\:\gamma}}} \\ $$$${similarly} \\ $$$$\Rightarrow{y}=\frac{{ca}\:\mathrm{sin}\:\left(\beta−\angle{B}\right)}{\mathrm{sin}\:\gamma\:\mathrm{sin}\:\alpha\:\sqrt{\frac{{c}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\gamma}+\frac{{a}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\alpha}+\frac{\mathrm{2}{ca}\:\mathrm{cos}\:\left(\beta−\angle{B}\right)\:}{\mathrm{sin}\:\gamma\:\mathrm{sin}\:{a}}}} \\ $$$$\Rightarrow{z}=\frac{{ab}\:\mathrm{sin}\:\left(\gamma−\angle{C}\right)}{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta\:\sqrt{\frac{{a}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\alpha}+\frac{{b}^{\mathrm{2}} }{\mathrm{sin}^{\mathrm{2}} \:\beta}+\frac{\mathrm{2}{ab}\:\mathrm{cos}\:\left(\gamma−\angle{C}\right)\:}{\mathrm{sin}\:\alpha\:\mathrm{sin}\:\beta}}} \\ $$$${example}: \\ $$$${a}=\mathrm{12},\:{b}=\mathrm{8},\:{c}=\mathrm{10} \\ $$$$\alpha=\mathrm{120}°,\:\beta=\mathrm{90}°,\:\gamma=\mathrm{150}° \\ $$$$\mathrm{cos}\:\angle{C}=\frac{\mathrm{12}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} }{\mathrm{2}×\mathrm{12}×\mathrm{8}}=\frac{\mathrm{9}}{\mathrm{16}} \\ $$$$\mathrm{sin}\:\left(\gamma−\angle{C}\right)=\frac{\mathrm{9}+\mathrm{5}\sqrt{\mathrm{21}}}{\mathrm{32}} \\ $$$$\mathrm{cos}\:\left(\gamma−\angle{C}\right)=\frac{−\mathrm{9}\sqrt{\mathrm{3}}+\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{32}} \\ $$$${z}=\frac{\mathrm{12}×\mathrm{8}×\frac{\mathrm{9}+\mathrm{5}\sqrt{\mathrm{21}}}{\mathrm{32}}}{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\sqrt{\frac{\mathrm{12}^{\mathrm{2}} ×\mathrm{4}}{\mathrm{3}}+\mathrm{8}^{\mathrm{2}} +\frac{\mathrm{2}×\mathrm{12}×\mathrm{8}×\mathrm{2}\:}{\:\sqrt{\mathrm{3}}}×\frac{−\mathrm{9}\sqrt{\mathrm{3}}+\mathrm{5}\sqrt{\mathrm{7}}}{\mathrm{32}}}} \\ $$$$\:\:=\frac{\mathrm{9}\sqrt{\mathrm{3}}+\mathrm{15}\sqrt{\mathrm{7}}}{\:\sqrt{\mathrm{37}+\mathrm{5}\sqrt{\mathrm{21}}}}\approx\mathrm{7}.\mathrm{141} \\ $$
Commented by mr W last updated on 01/May/24

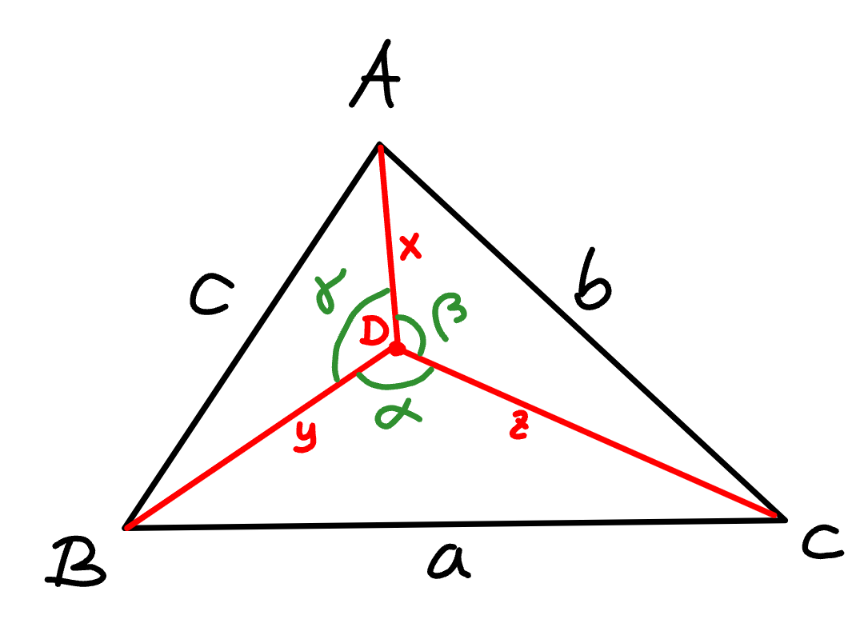
$${geometrically}\:{it}\:{is}\:{to}\:{find}\:{the} \\ $$$${distances}\:{from}\:{a}\:{point}\:{inside}\:{a} \\ $$$${triangle}\:{to}\:{the}\:{vertexes}\:{of}\:{the}\:{triangle}. \\ $$$${when}\:\alpha=\beta=\gamma=\mathrm{120}°,\:{this}\:{point}\:{is} \\ $$$${the}\:{so}−{called}\:{fermat}\:{point}. \\ $$
