
Question Number 66619 by mr W last updated on 17/Aug/19
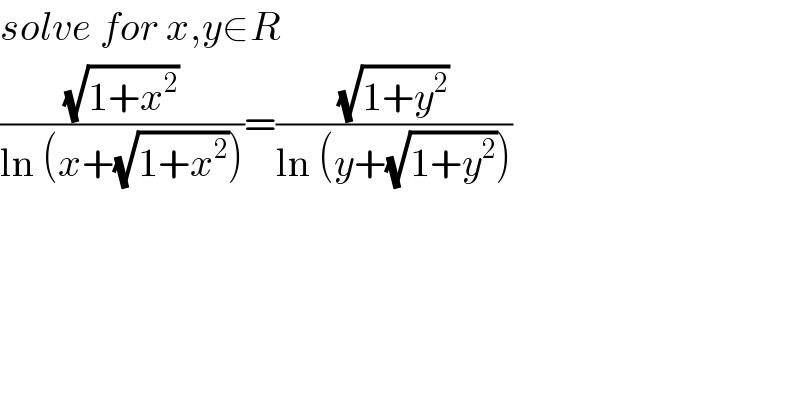
$${solve}\:{for}\:{x},{y}\in{R} \\ $$$$\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)}=\frac{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }}{\mathrm{ln}\:\left({y}+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\right)} \\ $$
Answered by Smail last updated on 17/Aug/19
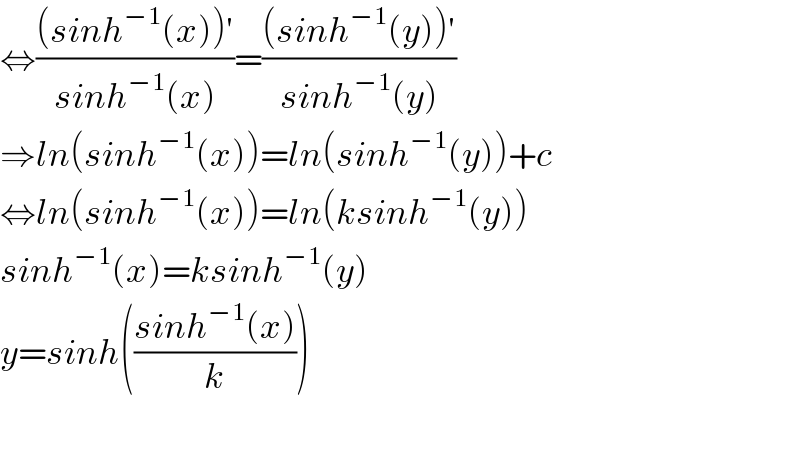
$$\Leftrightarrow\frac{\left({sinh}^{−\mathrm{1}} \left({x}\right)\right)'}{{sinh}^{−\mathrm{1}} \left({x}\right)}=\frac{\left({sinh}^{−\mathrm{1}} \left({y}\right)\right)'}{{sinh}^{−\mathrm{1}} \left({y}\right)} \\ $$$$\Rightarrow{ln}\left({sinh}^{−\mathrm{1}} \left({x}\right)\right)={ln}\left({sinh}^{−\mathrm{1}} \left({y}\right)\right)+{c} \\ $$$$\Leftrightarrow{ln}\left({sinh}^{−\mathrm{1}} \left({x}\right)\right)={ln}\left({ksinh}^{−\mathrm{1}} \left({y}\right)\right) \\ $$$${sinh}^{−\mathrm{1}} \left({x}\right)={ksinh}^{−\mathrm{1}} \left({y}\right) \\ $$$${y}={sinh}\left(\frac{{sinh}^{−\mathrm{1}} \left({x}\right)}{{k}}\right) \\ $$$$ \\ $$
Commented by mr W last updated on 17/Aug/19

$${thank}\:{you}\:{sir}! \\ $$
Commented by mr W last updated on 18/Aug/19
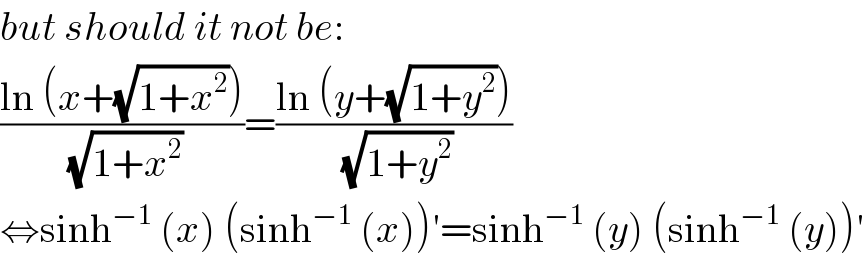
$${but}\:{should}\:{it}\:{not}\:{be}: \\ $$$$\frac{\mathrm{ln}\:\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\frac{\mathrm{ln}\:\left({y}+\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\right)}{\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }} \\ $$$$\Leftrightarrow\mathrm{sinh}^{−\mathrm{1}} \:\left({x}\right)\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\left({x}\right)\right)'=\mathrm{sinh}^{−\mathrm{1}} \:\left({y}\right)\:\left(\mathrm{sinh}^{−\mathrm{1}} \:\left({y}\right)\right)' \\ $$
