Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 75932 by Rio Michael last updated on 21/Dec/19

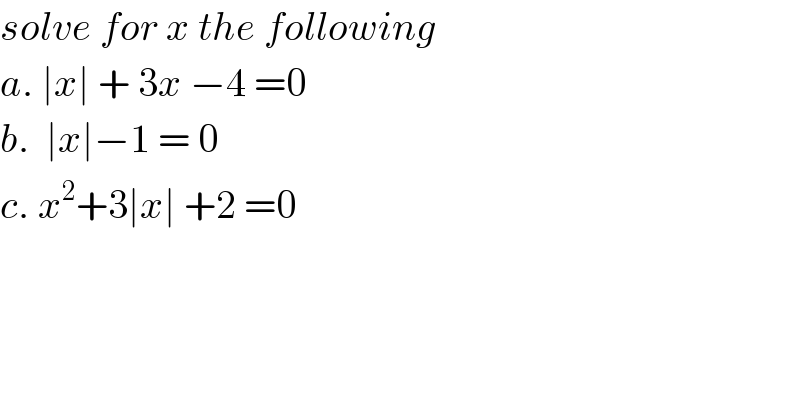
solve for x the following a. ∣x∣ + 3x −4 =0 b. ∣x∣−1 = 0 c. x^2 +3∣x∣ +2 =0

$${solve}\:{for}\:{x}\:{the}\:{following} \\ $$$${a}.\:\mid{x}\mid\:+\:\mathrm{3}{x}\:−\mathrm{4}\:=\mathrm{0} \\ $$$${b}.\:\:\mid{x}\mid−\mathrm{1}\:=\:\mathrm{0} \\ $$$${c}.\:{x}^{\mathrm{2}} +\mathrm{3}\mid{x}\mid\:+\mathrm{2}\:=\mathrm{0} \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 21/Dec/19

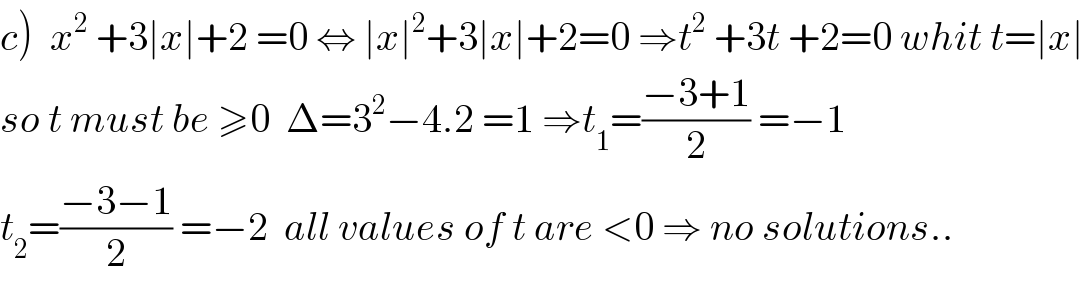
c) x^2 +3∣x∣+2 =0 ⇔ ∣x∣^2 +3∣x∣+2=0 ⇒t^2 +3t +2=0 whit t=∣x∣ so t must be ≥0 Δ=3^2 −4.2 =1 ⇒t_1 =((−3+1)/2) =−1 t_2 =((−3−1)/2) =−2 all values of t are <0 ⇒ no solutions..

$$\left.{c}\right)\:\:{x}^{\mathrm{2}} \:+\mathrm{3}\mid{x}\mid+\mathrm{2}\:=\mathrm{0}\:\Leftrightarrow\:\mid{x}\mid^{\mathrm{2}} +\mathrm{3}\mid{x}\mid+\mathrm{2}=\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} \:+\mathrm{3}{t}\:+\mathrm{2}=\mathrm{0}\:{whit}\:{t}=\mid{x}\mid \\ $$$${so}\:{t}\:{must}\:{be}\:\geqslant\mathrm{0}\:\:\Delta=\mathrm{3}^{\mathrm{2}} −\mathrm{4}.\mathrm{2}\:=\mathrm{1}\:\Rightarrow{t}_{\mathrm{1}} =\frac{−\mathrm{3}+\mathrm{1}}{\mathrm{2}}\:=−\mathrm{1} \\ $$$${t}_{\mathrm{2}} =\frac{−\mathrm{3}−\mathrm{1}}{\mathrm{2}}\:=−\mathrm{2}\:\:{all}\:{values}\:{of}\:{t}\:{are}\:<\mathrm{0}\:\Rightarrow\:{no}\:{solutions}.. \\ $$

Answered by benjo last updated on 21/Dec/19

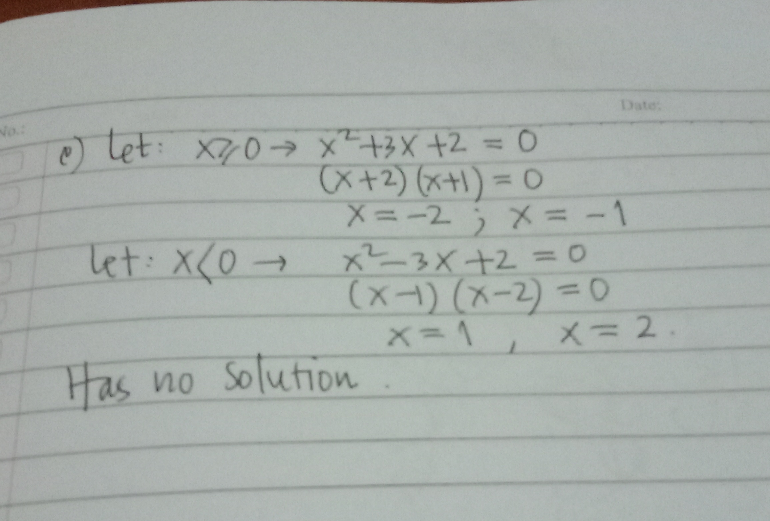
Commented by Rio Michael last updated on 21/Dec/19

why sir

$${why}\:{sir} \\ $$

Commented by mr W last updated on 22/Dec/19

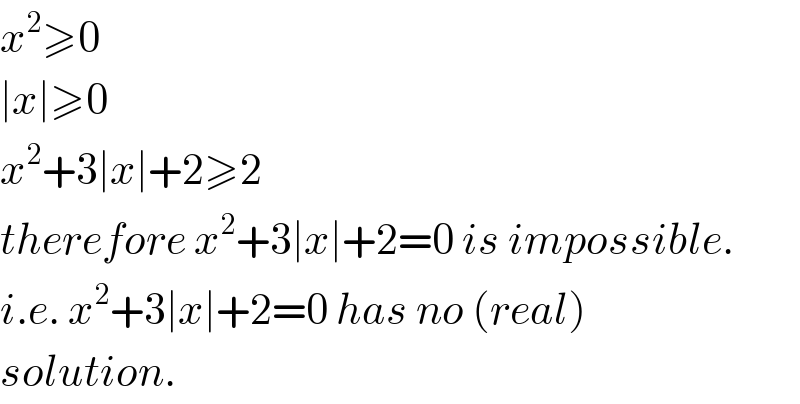
x^2 ≥0 ∣x∣≥0 x^2 +3∣x∣+2≥2 therefore x^2 +3∣x∣+2=0 is impossible. i.e. x^2 +3∣x∣+2=0 has no (real) solution.

$${x}^{\mathrm{2}} \geqslant\mathrm{0} \\ $$$$\mid{x}\mid\geqslant\mathrm{0} \\ $$$${x}^{\mathrm{2}} +\mathrm{3}\mid{x}\mid+\mathrm{2}\geqslant\mathrm{2} \\ $$$${therefore}\:{x}^{\mathrm{2}} +\mathrm{3}\mid{x}\mid+\mathrm{2}=\mathrm{0}\:{is}\:{impossible}. \\ $$$${i}.{e}.\:{x}^{\mathrm{2}} +\mathrm{3}\mid{x}\mid+\mathrm{2}=\mathrm{0}\:{has}\:{no}\:\left({real}\right) \\ $$$${solution}. \\ $$

Commented by benjo last updated on 24/Dec/19

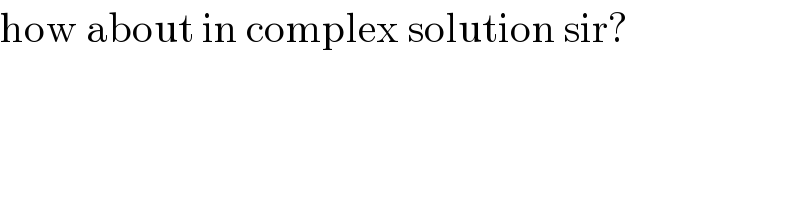
how about in complex solution sir?

$$\mathrm{how}\:\mathrm{about}\:\mathrm{in}\:\mathrm{complex}\:\mathrm{solution}\:\mathrm{sir}? \\ $$

Commented by mr W last updated on 24/Dec/19

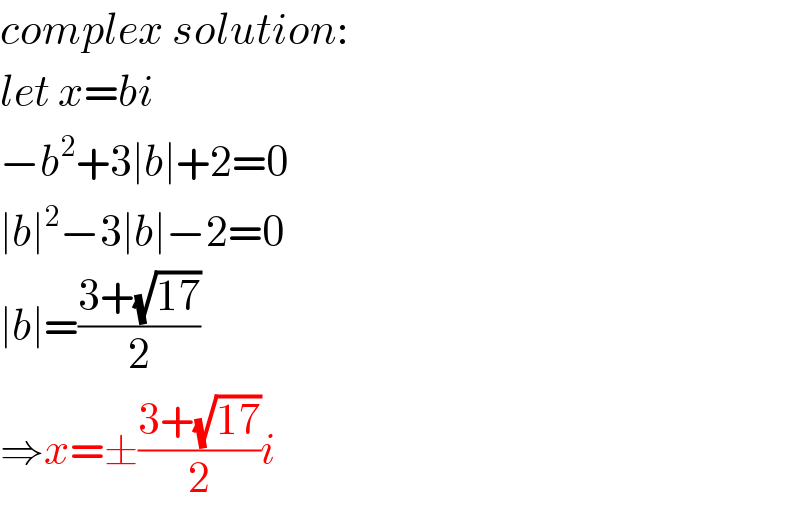
complex solution: let x=bi −b^2 +3∣b∣+2=0 ∣b∣^2 −3∣b∣−2=0 ∣b∣=((3+(√(17)))/2) ⇒x=±((3+(√(17)))/2)i

$${complex}\:{solution}: \\ $$$${let}\:{x}={bi} \\ $$$$−{b}^{\mathrm{2}} +\mathrm{3}\mid{b}\mid+\mathrm{2}=\mathrm{0} \\ $$$$\mid{b}\mid^{\mathrm{2}} −\mathrm{3}\mid{b}\mid−\mathrm{2}=\mathrm{0} \\ $$$$\mid{b}\mid=\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}} \\ $$$$\Rightarrow{x}=\pm\frac{\mathrm{3}+\sqrt{\mathrm{17}}}{\mathrm{2}}{i} \\ $$

Commented by benjo last updated on 24/Dec/19

thanks you sir

$$\mathrm{thanks}\:\mathrm{you}\:\mathrm{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com