
Question Number 189610 by Spillover last updated on 19/Mar/23
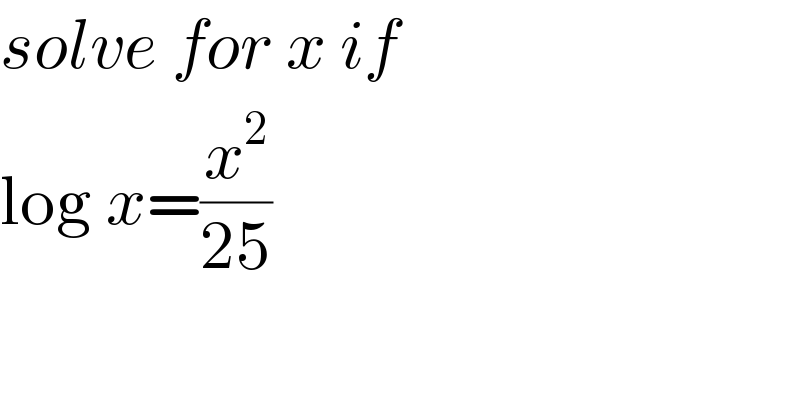
$${solve}\:{for}\:{x}\:{if}\:\:\: \\ $$$$\mathrm{log}\:{x}=\frac{{x}^{\mathrm{2}} }{\mathrm{25}} \\ $$
Answered by mr W last updated on 19/Mar/23
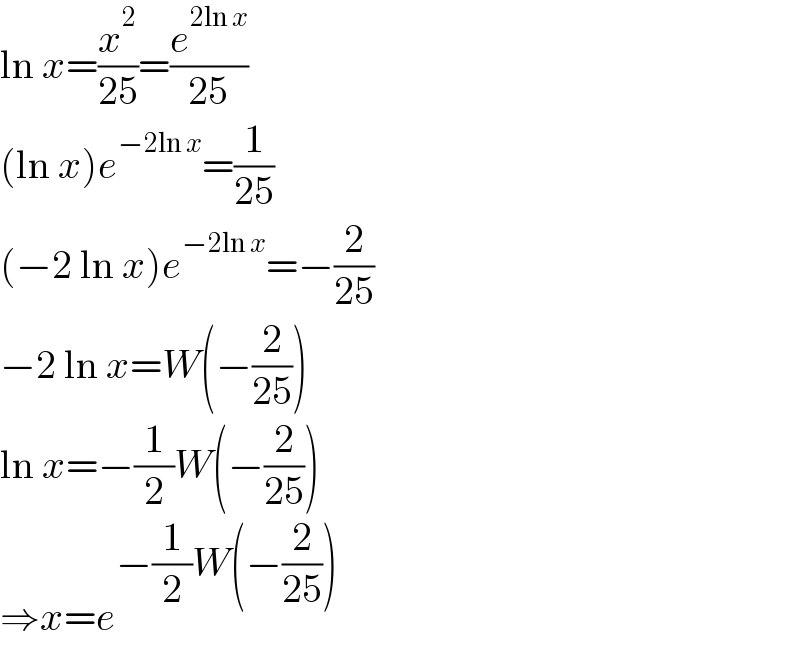
$$\mathrm{ln}\:{x}=\frac{{x}^{\mathrm{2}} }{\mathrm{25}}=\frac{{e}^{\mathrm{2ln}\:{x}} }{\mathrm{25}} \\ $$$$\left(\mathrm{ln}\:{x}\right){e}^{−\mathrm{2ln}\:{x}} =\frac{\mathrm{1}}{\mathrm{25}} \\ $$$$\left(−\mathrm{2}\:\mathrm{ln}\:{x}\right){e}^{−\mathrm{2ln}\:{x}} =−\frac{\mathrm{2}}{\mathrm{25}} \\ $$$$−\mathrm{2}\:\mathrm{ln}\:{x}={W}\left(−\frac{\mathrm{2}}{\mathrm{25}}\right) \\ $$$$\mathrm{ln}\:{x}=−\frac{\mathrm{1}}{\mathrm{2}}{W}\left(−\frac{\mathrm{2}}{\mathrm{25}}\right) \\ $$$$\Rightarrow{x}={e}^{−\frac{\mathrm{1}}{\mathrm{2}}{W}\left(−\frac{\mathrm{2}}{\mathrm{25}}\right)} \\ $$
