Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 153803 by weltr last updated on 10/Sep/21

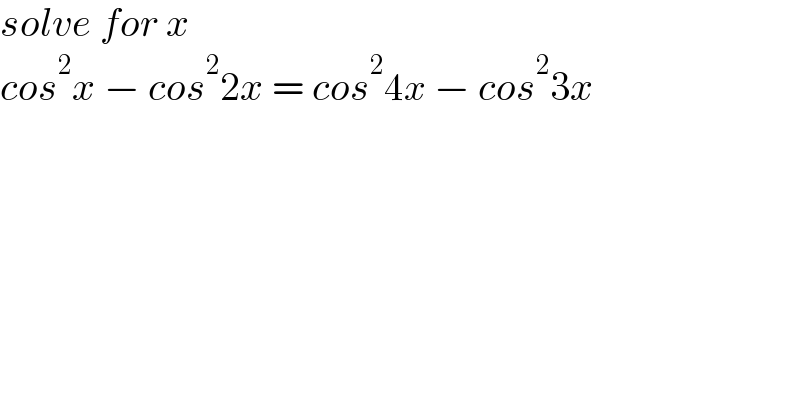
solve for x cos^2 x − cos^2 2x = cos^2 4x − cos^2 3x

$${solve}\:{for}\:{x} \\ $$$${cos}^{\mathrm{2}} {x}\:−\:{cos}^{\mathrm{2}} \mathrm{2}{x}\:=\:{cos}^{\mathrm{2}} \mathrm{4}{x}\:−\:{cos}^{\mathrm{2}} \mathrm{3}{x} \\ $$

Commented by Ar Brandon last updated on 10/Sep/21

x=0[π] is a solution

$${x}=\mathrm{0}\left[\pi\right]\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$

Answered by puissant last updated on 10/Sep/21

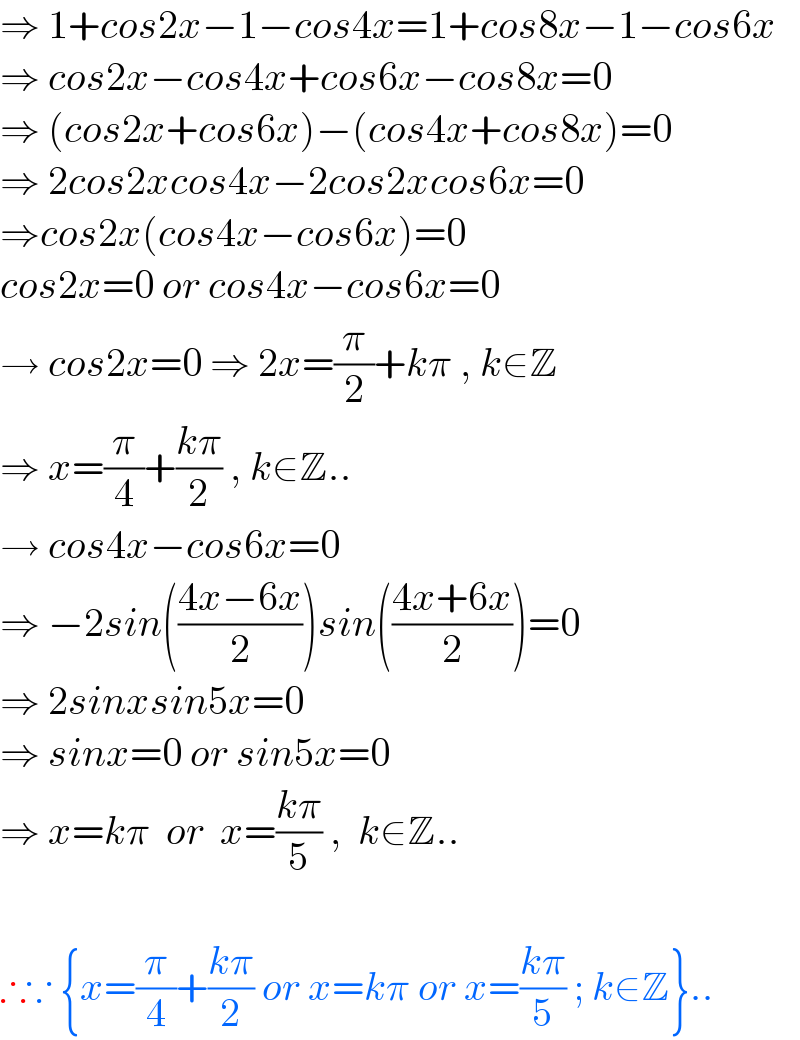
⇒ 1+cos2x−1−cos4x=1+cos8x−1−cos6x ⇒ cos2x−cos4x+cos6x−cos8x=0 ⇒ (cos2x+cos6x)−(cos4x+cos8x)=0 ⇒ 2cos2xcos4x−2cos2xcos6x=0 ⇒cos2x(cos4x−cos6x)=0 cos2x=0 or cos4x−cos6x=0 → cos2x=0 ⇒ 2x=(π/2)+kπ , k∈Z ⇒ x=(π/4)+((kπ)/2) , k∈Z.. → cos4x−cos6x=0 ⇒ −2sin(((4x−6x)/2))sin(((4x+6x)/2))=0 ⇒ 2sinxsin5x=0 ⇒ sinx=0 or sin5x=0 ⇒ x=kπ or x=((kπ)/5) , k∈Z.. ∴∵ {x=(π/4)+((kπ)/2) or x=kπ or x=((kπ)/5) ; k∈Z}..

$$\Rightarrow\:\mathrm{1}+{cos}\mathrm{2}{x}−\mathrm{1}−{cos}\mathrm{4}{x}=\mathrm{1}+{cos}\mathrm{8}{x}−\mathrm{1}−{cos}\mathrm{6}{x} \\ $$$$\Rightarrow\:{cos}\mathrm{2}{x}−{cos}\mathrm{4}{x}+{cos}\mathrm{6}{x}−{cos}\mathrm{8}{x}=\mathrm{0} \\ $$$$\Rightarrow\:\left({cos}\mathrm{2}{x}+{cos}\mathrm{6}{x}\right)−\left({cos}\mathrm{4}{x}+{cos}\mathrm{8}{x}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}{cos}\mathrm{2}{xcos}\mathrm{4}{x}−\mathrm{2}{cos}\mathrm{2}{xcos}\mathrm{6}{x}=\mathrm{0} \\ $$$$\Rightarrow{cos}\mathrm{2}{x}\left({cos}\mathrm{4}{x}−{cos}\mathrm{6}{x}\right)=\mathrm{0} \\ $$$${cos}\mathrm{2}{x}=\mathrm{0}\:{or}\:{cos}\mathrm{4}{x}−{cos}\mathrm{6}{x}=\mathrm{0} \\ $$$$\rightarrow\:{cos}\mathrm{2}{x}=\mathrm{0}\:\Rightarrow\:\mathrm{2}{x}=\frac{\pi}{\mathrm{2}}+{k}\pi\:,\:{k}\in\mathbb{Z} \\ $$$$\Rightarrow\:{x}=\frac{\pi}{\mathrm{4}}+\frac{{k}\pi}{\mathrm{2}}\:,\:{k}\in\mathbb{Z}.. \\ $$$$\rightarrow\:{cos}\mathrm{4}{x}−{cos}\mathrm{6}{x}=\mathrm{0} \\ $$$$\Rightarrow\:−\mathrm{2}{sin}\left(\frac{\mathrm{4}{x}−\mathrm{6}{x}}{\mathrm{2}}\right){sin}\left(\frac{\mathrm{4}{x}+\mathrm{6}{x}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{2}{sinxsin}\mathrm{5}{x}=\mathrm{0} \\ $$$$\Rightarrow\:{sinx}=\mathrm{0}\:{or}\:{sin}\mathrm{5}{x}=\mathrm{0} \\ $$$$\Rightarrow\:{x}={k}\pi\:\:{or}\:\:{x}=\frac{{k}\pi}{\mathrm{5}}\:,\:\:{k}\in\mathbb{Z}.. \\ $$$$ \\ $$$$\therefore\because\:\left\{{x}=\frac{\pi}{\mathrm{4}}+\frac{{k}\pi}{\mathrm{2}}\:{or}\:{x}={k}\pi\:{or}\:{x}=\frac{{k}\pi}{\mathrm{5}}\:;\:{k}\in\mathbb{Z}\right\}.. \\ $$

Commented by weltr last updated on 10/Sep/21

thank you

$${thank}\:{you} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com