
Question Number 11543 by Nysiroke last updated on 28/Mar/17
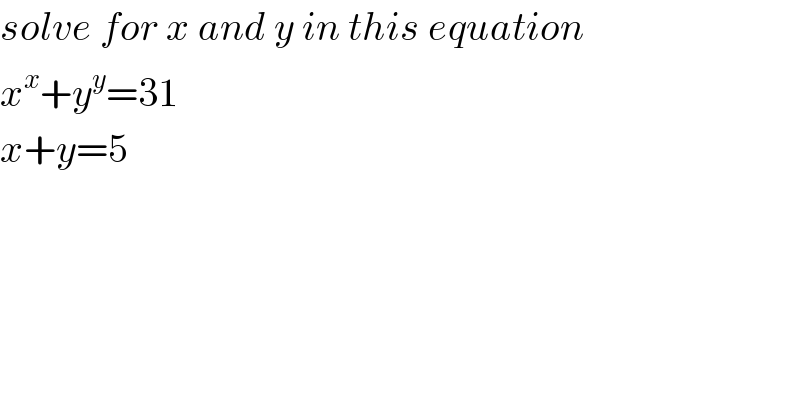
$${solve}\:{for}\:{x}\:{and}\:{y}\:{in}\:{this}\:{equation} \\ $$$${x}^{{x}} +{y}^{{y}} =\mathrm{31} \\ $$$${x}+{y}=\mathrm{5} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17
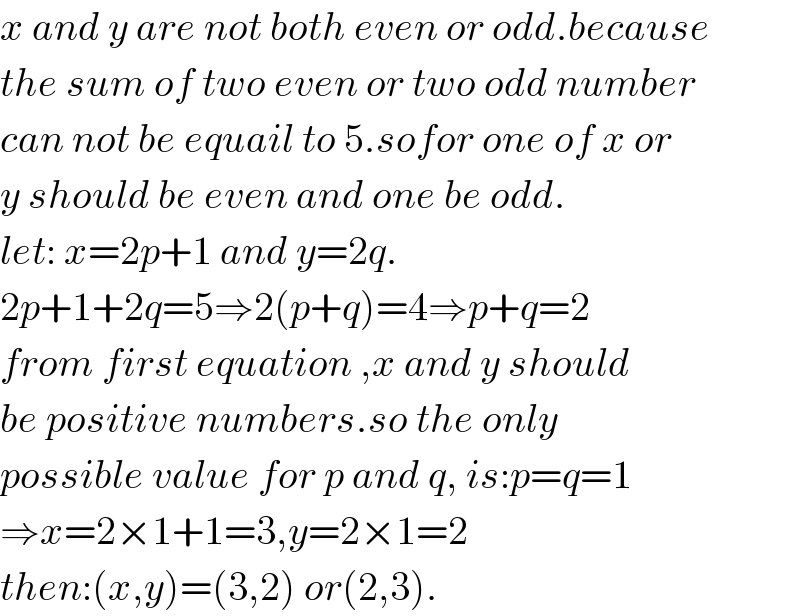
$${x}\:{and}\:{y}\:{are}\:{not}\:{both}\:{even}\:{or}\:{odd}.{because} \\ $$$${the}\:{sum}\:{of}\:{two}\:{even}\:{or}\:{two}\:{odd}\:{number} \\ $$$${can}\:{not}\:{be}\:{equail}\:{to}\:\mathrm{5}.{sofor}\:{one}\:{of}\:{x}\:{or} \\ $$$${y}\:{should}\:{be}\:{even}\:{and}\:{one}\:{be}\:{odd}. \\ $$$${let}:\:{x}=\mathrm{2}{p}+\mathrm{1}\:{and}\:{y}=\mathrm{2}{q}. \\ $$$$\mathrm{2}{p}+\mathrm{1}+\mathrm{2}{q}=\mathrm{5}\Rightarrow\mathrm{2}\left({p}+{q}\right)=\mathrm{4}\Rightarrow{p}+{q}=\mathrm{2} \\ $$$${from}\:{first}\:{equation}\:,{x}\:{and}\:{y}\:{should} \\ $$$${be}\:{positive}\:{numbers}.{so}\:{the}\:{only} \\ $$$${possible}\:{value}\:{for}\:{p}\:{and}\:{q},\:{is}:{p}={q}=\mathrm{1} \\ $$$$\Rightarrow{x}=\mathrm{2}×\mathrm{1}+\mathrm{1}=\mathrm{3},{y}=\mathrm{2}×\mathrm{1}=\mathrm{2} \\ $$$${then}:\left({x},{y}\right)=\left(\mathrm{3},\mathrm{2}\right)\:{or}\left(\mathrm{2},\mathrm{3}\right). \\ $$
Commented by Nysiroke last updated on 02/Apr/17
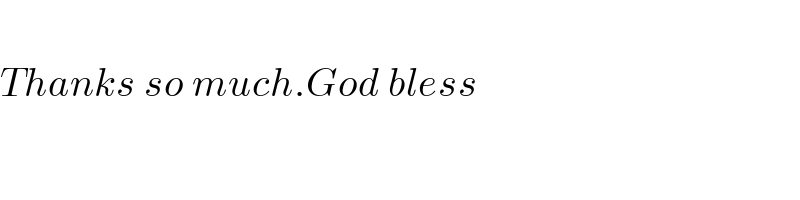
$$ \\ $$$${Thanks}\:{so}\:{much}.{God}\:{bless} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17

$$\left(\mathrm{3},\mathrm{2}\right),\left(\mathrm{2},\mathrm{3}\right)\:. \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 29/Mar/17

Commented by Nayon last updated on 29/Mar/17

$${can}\:{you}\:{give}\:{the}\:{app}\:{by}\:{which}\:{you} \\ $$$${drawn}\:{the}\:{graph}? \\ $$
Commented by b.e.h.i.8.3.4.1.7@gmail.com last updated on 30/Mar/17

$${geogebra} \\ $$
Commented by Nysiroke last updated on 02/Apr/17

$${Excellent}. \\ $$
