
Question Number 119997 by behi83417@gmail.com last updated on 28/Oct/20

$$\mathrm{solve}\:\mathrm{for}\:\mathrm{x},\mathrm{a}\in\boldsymbol{\mathrm{R}}. \\ $$$$\sqrt{\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{ax}}+\boldsymbol{{a}}^{\mathrm{2}} }+\sqrt{\boldsymbol{{x}}^{\mathrm{2}} −\boldsymbol{{ax}}+\boldsymbol{{a}}^{\mathrm{2}} }=\mathrm{1} \\ $$
Answered by Lordose last updated on 28/Oct/20

$$\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{a}^{\mathrm{2}} \:=\:\mathrm{1}\:−\:\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} }\:+\:\mathrm{x}^{\mathrm{2}} −\mathrm{ax}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} }\:=\:\mathrm{1}−\mathrm{x}^{\mathrm{2}} −\mathrm{ax}−\mathrm{a}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} \\ $$$$\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} \right)\:=\:\left(\mathrm{1}−\mathrm{2ax}\right)^{\mathrm{2}} \\ $$$$\mathrm{4x}^{\mathrm{2}} −\mathrm{4ax}+\mathrm{4a}^{\mathrm{2}} \:=\:\mathrm{1}\:−\:\mathrm{4ax}\:+\:\mathrm{4a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \\ $$$$\left(\mathrm{4}−\mathrm{4a}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{4a}^{\mathrm{2}} \:=\:\mathrm{1} \\ $$$$\mathrm{x}^{\mathrm{2}} \:=\:\frac{\mathrm{1}−\mathrm{4a}^{\mathrm{2}} }{\left(\mathrm{4}−\mathrm{4a}^{\mathrm{2}} \right)} \\ $$$$\mathrm{x}\:=\:\pm\frac{\sqrt{\mathrm{1}−\mathrm{4a}^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }} \\ $$
Commented by behi83417@gmail.com last updated on 28/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{sir}. \\ $$
Answered by TANMAY PANACEA last updated on 28/Oct/20
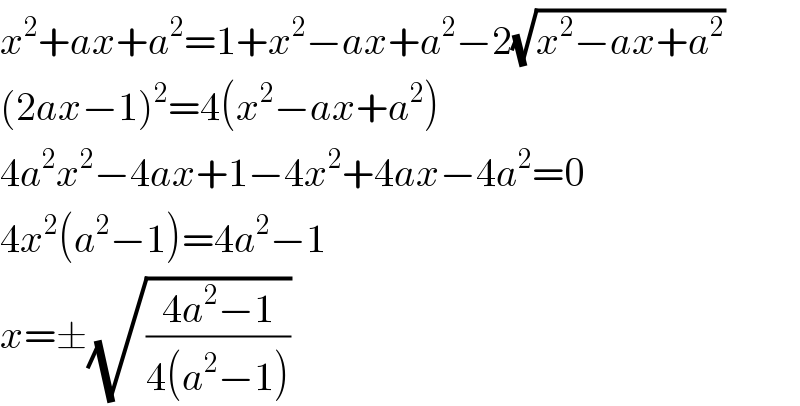
$${x}^{\mathrm{2}} +{ax}+{a}^{\mathrm{2}} =\mathrm{1}+{x}^{\mathrm{2}} −{ax}+{a}^{\mathrm{2}} −\mathrm{2}\sqrt{{x}^{\mathrm{2}} −{ax}+{a}^{\mathrm{2}} } \\ $$$$\left(\mathrm{2}{ax}−\mathrm{1}\right)^{\mathrm{2}} =\mathrm{4}\left({x}^{\mathrm{2}} −{ax}+{a}^{\mathrm{2}} \right) \\ $$$$\mathrm{4}{a}^{\mathrm{2}} {x}^{\mathrm{2}} −\mathrm{4}{ax}+\mathrm{1}−\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}{ax}−\mathrm{4}{a}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{4}{x}^{\mathrm{2}} \left({a}^{\mathrm{2}} −\mathrm{1}\right)=\mathrm{4}{a}^{\mathrm{2}} −\mathrm{1} \\ $$$${x}=\pm\sqrt{\frac{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{1}}{\mathrm{4}\left({a}^{\mathrm{2}} −\mathrm{1}\right)}}\: \\ $$
Commented by behi83417@gmail.com last updated on 28/Oct/20
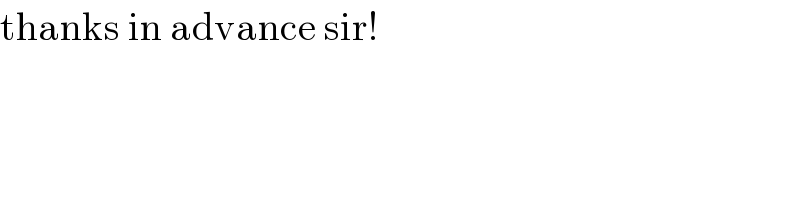
$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{sir}! \\ $$
Commented by TANMAY PANACEA last updated on 28/Oct/20

$${most}\:{welcome}\:{sir} \\ $$
Answered by behi83417@gmail.com last updated on 28/Oct/20

$$\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{a}^{\mathrm{2}} =\mathrm{u}^{\mathrm{2}} ,\mathrm{x}^{\mathrm{2}} −\mathrm{ax}+\mathrm{a}^{\mathrm{2}} =\mathrm{v}^{\mathrm{2}} \\ $$$$\Rightarrow\begin{cases}{\mathrm{u}+\mathrm{v}=\mathrm{1}}\\{\mathrm{u}^{\mathrm{2}} −\mathrm{v}^{\mathrm{2}} =\mathrm{2ax}}\end{cases}\Rightarrow\mathrm{u}−\mathrm{v}=\mathrm{2ax} \\ $$$$\Rightarrow\left(\mathrm{u}+\mathrm{v}\right)^{\mathrm{2}} −\mathrm{4uv}=\left(\mathrm{2ax}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{uv}=\frac{\mathrm{1}−\mathrm{4a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{4}},\mathrm{u}+\mathrm{v}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{z}^{\mathrm{2}} −\mathrm{z}+\frac{\mathrm{1}−\mathrm{4a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{z}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}−\left(\mathrm{1}−\mathrm{4a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)}}{\mathrm{2}}=\frac{\mathrm{1}\pm\mathrm{2ax}}{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{a}^{\mathrm{2}} }=\frac{\mathrm{1}\pm\mathrm{2ax}}{\mathrm{2}}\Rightarrow \\ $$$$\mathrm{4}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{ax}+\mathrm{a}^{\mathrm{2}} \right)=\mathrm{1}\pm\mathrm{4ax}+\mathrm{4a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \\ $$$$\Rightarrow\begin{cases}{\mathrm{4}\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} =\mathrm{1}−\mathrm{4a}^{\mathrm{2}} \Rightarrow\mathrm{x}=\pm\frac{\mathrm{1}}{\mathrm{2}}.\sqrt{\frac{\mathrm{1}−\mathrm{4a}^{\mathrm{2}} }{\mathrm{1}−\mathrm{a}^{\mathrm{2}} }}}\\{\mathrm{4x}^{\mathrm{2}} +\mathrm{4ax}+\mathrm{4a}^{\mathrm{2}} =\mathrm{1}−\mathrm{4ax}+\mathrm{4a}^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \Rightarrow}\end{cases} \\ $$$$\Rightarrow\mathrm{4}\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\mathrm{x}^{\mathrm{2}} +\mathrm{8ax}+\mathrm{4a}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\Rightarrow \\ $$$$\Rightarrow\mathrm{x}=\frac{−\mathrm{4a}\pm\sqrt{\mathrm{16a}^{\mathrm{2}} −\mathrm{4}\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)\left(\mathrm{4a}^{\mathrm{2}} −\mathrm{1}\right)}}{\mathrm{4}\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)}= \\ $$$$=\frac{−\mathrm{2a}\pm\sqrt{\mathrm{4a}^{\mathrm{2}} −\left(\mathrm{4a}^{\mathrm{2}} −\mathrm{1}−\mathrm{4a}^{\mathrm{4}} +\mathrm{a}^{\mathrm{2}} \right)}}{\mathrm{2}\left(\mathrm{1}−\mathrm{a}^{\mathrm{2}} \right)}= \\ $$$$=\frac{\mathrm{2a}\pm\sqrt{\mathrm{4a}^{\mathrm{4}} −\mathrm{a}^{\mathrm{2}} +\mathrm{1}}}{\mathrm{2}\left(\mathrm{a}^{\mathrm{2}} −\mathrm{1}\right)}\:\:\:\:.\blacksquare \\ $$
Answered by MJS_new last updated on 29/Oct/20
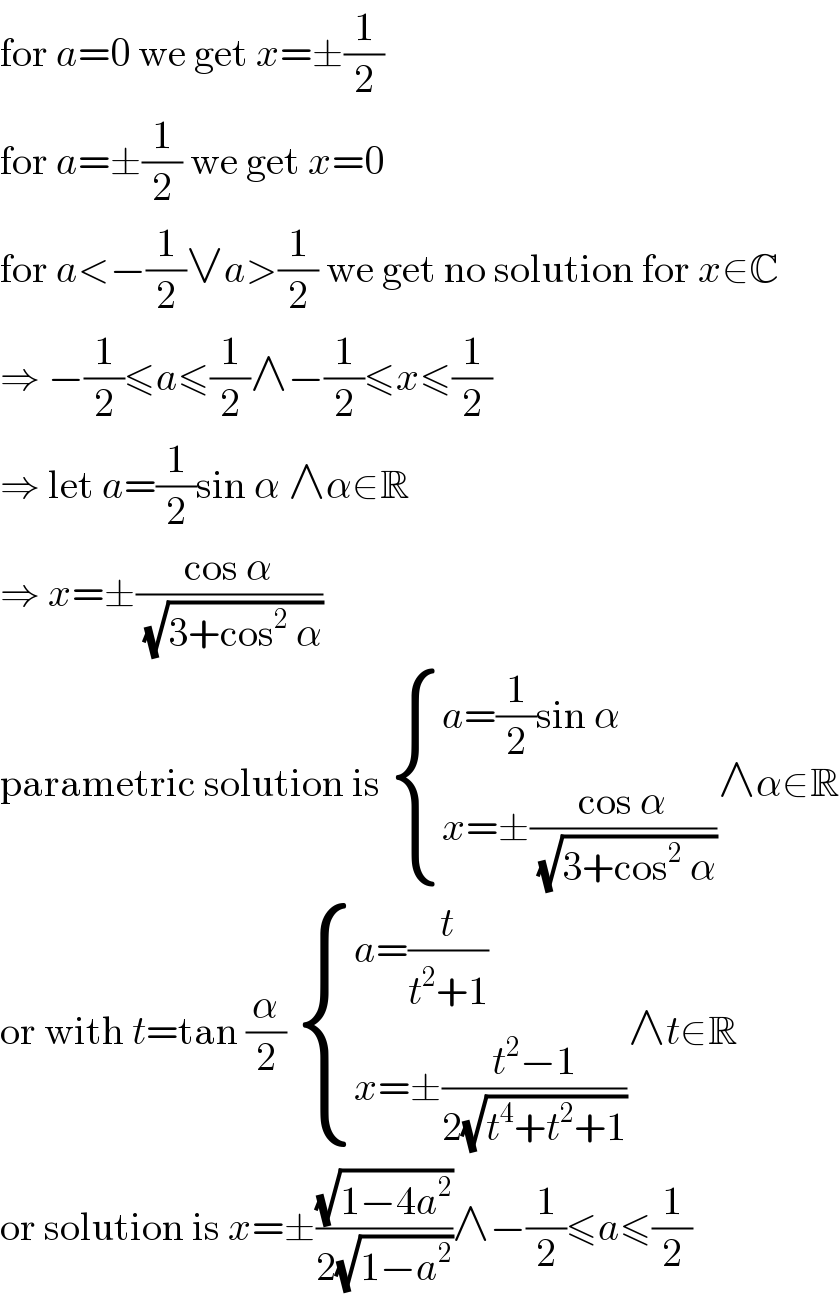
$$\mathrm{for}\:{a}=\mathrm{0}\:\mathrm{we}\:\mathrm{get}\:{x}=\pm\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{for}\:{a}=\pm\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{get}\:{x}=\mathrm{0} \\ $$$$\mathrm{for}\:{a}<−\frac{\mathrm{1}}{\mathrm{2}}\vee{a}>\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{we}\:\mathrm{get}\:\mathrm{no}\:\mathrm{solution}\:\mathrm{for}\:{x}\in\mathbb{C} \\ $$$$\Rightarrow\:−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{a}\leqslant\frac{\mathrm{1}}{\mathrm{2}}\wedge−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{let}\:{a}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\alpha\:\wedge\alpha\in\mathbb{R} \\ $$$$\Rightarrow\:{x}=\pm\frac{\mathrm{cos}\:\alpha}{\:\sqrt{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:\alpha}} \\ $$$$\mathrm{parametric}\:\mathrm{solution}\:\mathrm{is}\:\begin{cases}{{a}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\alpha}\\{{x}=\pm\frac{\mathrm{cos}\:\alpha}{\:\sqrt{\mathrm{3}+\mathrm{cos}^{\mathrm{2}} \:\alpha}}}\end{cases}\wedge\alpha\in\mathbb{R} \\ $$$$\mathrm{or}\:\mathrm{with}\:{t}=\mathrm{tan}\:\frac{\alpha}{\mathrm{2}}\:\begin{cases}{{a}=\frac{{t}}{{t}^{\mathrm{2}} +\mathrm{1}}}\\{{x}=\pm\frac{{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}\sqrt{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\mathrm{1}}}}\end{cases}\wedge{t}\in\mathbb{R} \\ $$$$\mathrm{or}\:\mathrm{solution}\:\mathrm{is}\:{x}=\pm\frac{\sqrt{\mathrm{1}−\mathrm{4}{a}^{\mathrm{2}} }}{\mathrm{2}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }}\wedge−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{a}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by behi83417@gmail.com last updated on 29/Oct/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{proph}:\mathrm{MJS} \\ $$$$\mathrm{please}\:\mathrm{let}\:\mathrm{me}\:\mathrm{know}\:\mathrm{what}\:\mathrm{you}\:\mathrm{think} \\ $$$$\mathrm{about}\:\mathrm{my}\:\mathrm{answer}. \\ $$
