
Question Number 173732 by mr W last updated on 17/Jul/22
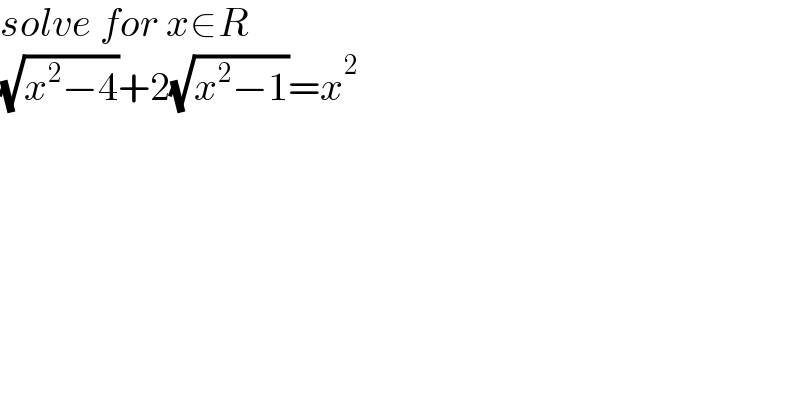
$${solve}\:{for}\:{x}\in{R} \\ $$$$\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}={x}^{\mathrm{2}} \\ $$
Commented by dragan91 last updated on 18/Jul/22
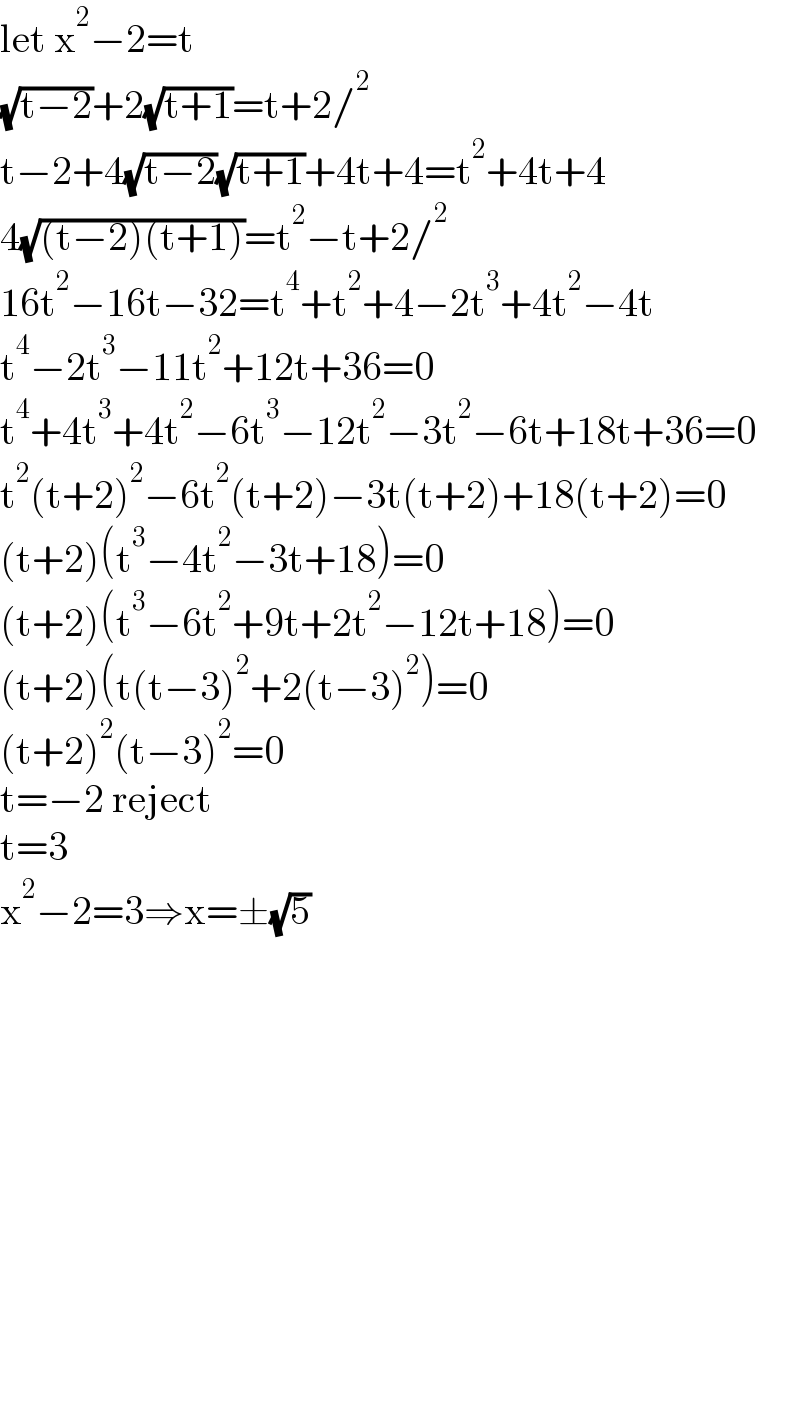
$$\mathrm{let}\:\mathrm{x}^{\mathrm{2}} −\mathrm{2}=\mathrm{t} \\ $$$$\sqrt{\mathrm{t}−\mathrm{2}}+\mathrm{2}\sqrt{\mathrm{t}+\mathrm{1}}=\mathrm{t}+\mathrm{2}/^{\mathrm{2}} \\ $$$$\mathrm{t}−\mathrm{2}+\mathrm{4}\sqrt{\mathrm{t}−\mathrm{2}}\sqrt{\mathrm{t}+\mathrm{1}}+\mathrm{4t}+\mathrm{4}=\mathrm{t}^{\mathrm{2}} +\mathrm{4t}+\mathrm{4} \\ $$$$\mathrm{4}\sqrt{\left(\mathrm{t}−\mathrm{2}\right)\left(\mathrm{t}+\mathrm{1}\right)}=\mathrm{t}^{\mathrm{2}} −\mathrm{t}+\mathrm{2}/^{\mathrm{2}} \\ $$$$\mathrm{16t}^{\mathrm{2}} −\mathrm{16t}−\mathrm{32}=\mathrm{t}^{\mathrm{4}} +\mathrm{t}^{\mathrm{2}} +\mathrm{4}−\mathrm{2t}^{\mathrm{3}} +\mathrm{4t}^{\mathrm{2}} −\mathrm{4t} \\ $$$$\mathrm{t}^{\mathrm{4}} −\mathrm{2t}^{\mathrm{3}} −\mathrm{11t}^{\mathrm{2}} +\mathrm{12t}+\mathrm{36}=\mathrm{0} \\ $$$$\mathrm{t}^{\mathrm{4}} +\mathrm{4t}^{\mathrm{3}} +\mathrm{4t}^{\mathrm{2}} −\mathrm{6t}^{\mathrm{3}} −\mathrm{12t}^{\mathrm{2}} −\mathrm{3t}^{\mathrm{2}} −\mathrm{6t}+\mathrm{18t}+\mathrm{36}=\mathrm{0} \\ $$$$\mathrm{t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{2}} −\mathrm{6t}^{\mathrm{2}} \left(\mathrm{t}+\mathrm{2}\right)−\mathrm{3t}\left(\mathrm{t}+\mathrm{2}\right)+\mathrm{18}\left(\mathrm{t}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\left(\mathrm{t}+\mathrm{2}\right)\left(\mathrm{t}^{\mathrm{3}} −\mathrm{4t}^{\mathrm{2}} −\mathrm{3t}+\mathrm{18}\right)=\mathrm{0} \\ $$$$\left(\mathrm{t}+\mathrm{2}\right)\left(\mathrm{t}^{\mathrm{3}} −\mathrm{6t}^{\mathrm{2}} +\mathrm{9t}+\mathrm{2t}^{\mathrm{2}} −\mathrm{12t}+\mathrm{18}\right)=\mathrm{0} \\ $$$$\left(\mathrm{t}+\mathrm{2}\right)\left(\mathrm{t}\left(\mathrm{t}−\mathrm{3}\right)^{\mathrm{2}} +\mathrm{2}\left(\mathrm{t}−\mathrm{3}\right)^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\left(\mathrm{t}+\mathrm{2}\right)^{\mathrm{2}} \left(\mathrm{t}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{t}=−\mathrm{2}\:\mathrm{reject} \\ $$$$\mathrm{t}=\mathrm{3}\: \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{2}=\mathrm{3}\Rightarrow\mathrm{x}=\pm\sqrt{\mathrm{5}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Skabetix last updated on 17/Jul/22
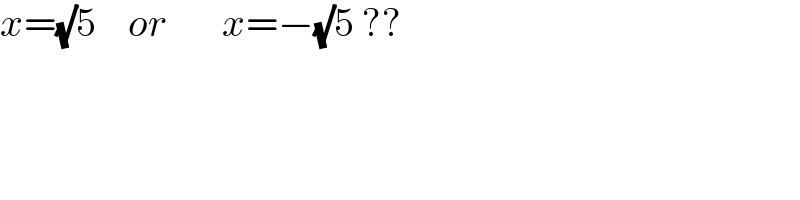
$${x}=\sqrt{}\mathrm{5}\:\:\:\:{or}\:\:\:\:\:\:\:{x}=−\sqrt{}\mathrm{5}\:?? \\ $$
Answered by mindispower last updated on 17/Jul/22
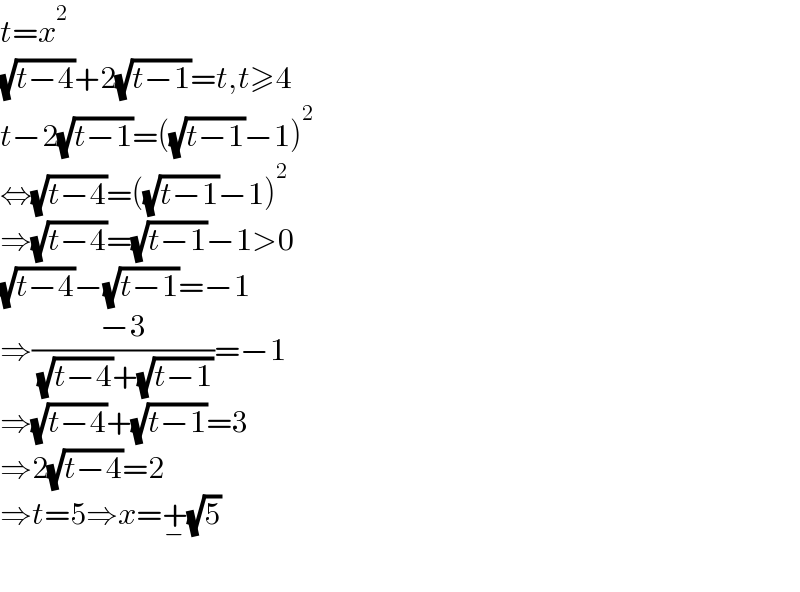
$${t}={x}^{\mathrm{2}} \\ $$$$\sqrt{{t}−\mathrm{4}}+\mathrm{2}\sqrt{{t}−\mathrm{1}}={t},{t}\geqslant\mathrm{4} \\ $$$${t}−\mathrm{2}\sqrt{{t}−\mathrm{1}}=\left(\sqrt{{t}−\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Leftrightarrow\sqrt{{t}−\mathrm{4}}=\left(\sqrt{{t}−\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{{t}−\mathrm{4}}=\sqrt{{t}−\mathrm{1}}−\mathrm{1}>\mathrm{0} \\ $$$$\sqrt{{t}−\mathrm{4}}−\sqrt{{t}−\mathrm{1}}=−\mathrm{1} \\ $$$$\Rightarrow\frac{−\mathrm{3}}{\:\sqrt{{t}−\mathrm{4}}+\sqrt{{t}−\mathrm{1}}}=−\mathrm{1} \\ $$$$\Rightarrow\sqrt{{t}−\mathrm{4}}+\sqrt{{t}−\mathrm{1}}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{2}\sqrt{{t}−\mathrm{4}}=\mathrm{2} \\ $$$$\Rightarrow{t}=\mathrm{5}\Rightarrow{x}=\underset{−} {+}\sqrt{\mathrm{5}} \\ $$$$ \\ $$
Commented by mr W last updated on 17/Jul/22
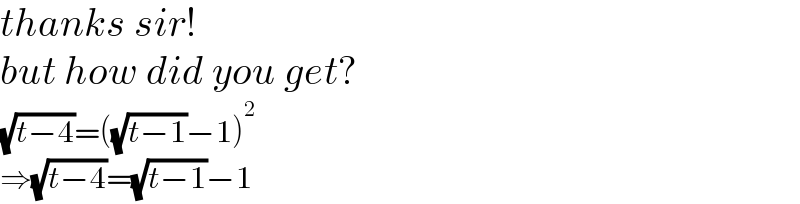
$${thanks}\:{sir}! \\ $$$${but}\:{how}\:{did}\:{you}\:{get}? \\ $$$$\sqrt{{t}−\mathrm{4}}=\left(\sqrt{{t}−\mathrm{1}}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\sqrt{{t}−\mathrm{4}}=\sqrt{{t}−\mathrm{1}}−\mathrm{1} \\ $$
Commented by Tawa11 last updated on 17/Jul/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
Answered by behi834171 last updated on 17/Jul/22
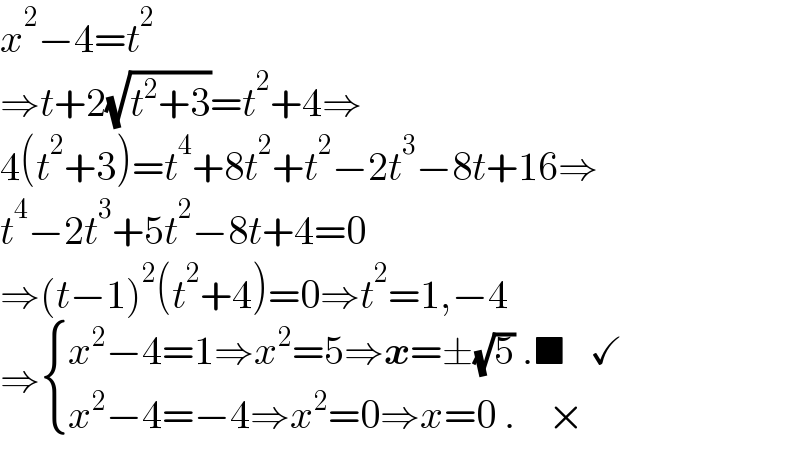
$${x}^{\mathrm{2}} −\mathrm{4}={t}^{\mathrm{2}} \\ $$$$\Rightarrow{t}+\mathrm{2}\sqrt{{t}^{\mathrm{2}} +\mathrm{3}}={t}^{\mathrm{2}} +\mathrm{4}\Rightarrow \\ $$$$\mathrm{4}\left({t}^{\mathrm{2}} +\mathrm{3}\right)={t}^{\mathrm{4}} +\mathrm{8}{t}^{\mathrm{2}} +{t}^{\mathrm{2}} −\mathrm{2}{t}^{\mathrm{3}} −\mathrm{8}{t}+\mathrm{16}\Rightarrow \\ $$$${t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} +\mathrm{5}{t}^{\mathrm{2}} −\mathrm{8}{t}+\mathrm{4}=\mathrm{0} \\ $$$$\Rightarrow\left({t}−\mathrm{1}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{4}\right)=\mathrm{0}\Rightarrow{t}^{\mathrm{2}} =\mathrm{1},−\mathrm{4} \\ $$$$\Rightarrow\begin{cases}{{x}^{\mathrm{2}} −\mathrm{4}=\mathrm{1}\Rightarrow{x}^{\mathrm{2}} =\mathrm{5}\Rightarrow\boldsymbol{{x}}=\pm\sqrt{\mathrm{5}}\:.\blacksquare\:\:\:\checkmark}\\{{x}^{\mathrm{2}} −\mathrm{4}=−\mathrm{4}\Rightarrow{x}^{\mathrm{2}} =\mathrm{0}\Rightarrow{x}=\mathrm{0}\:.\:\:\:\:×}\end{cases} \\ $$
Answered by mr W last updated on 17/Jul/22
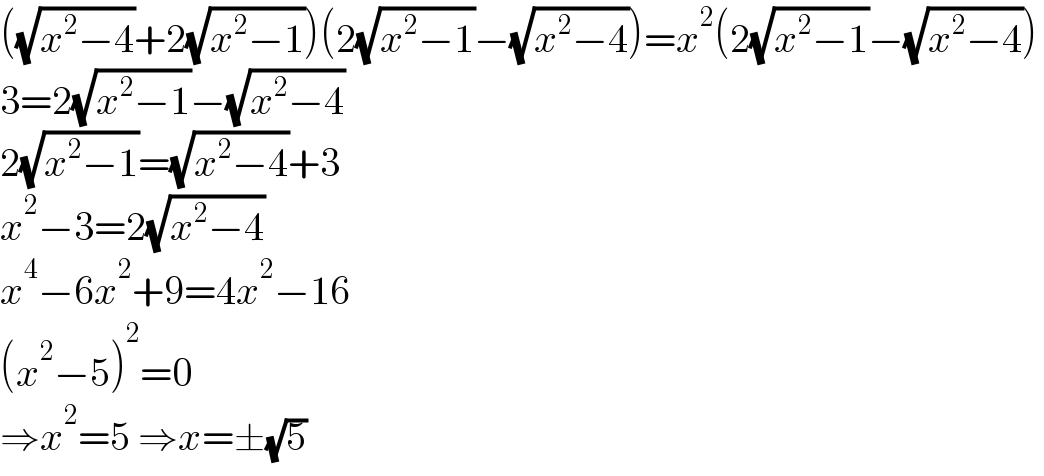
$$\left(\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}+\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right)\left(\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\right)={x}^{\mathrm{2}} \left(\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}\right) \\ $$$$\mathrm{3}=\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}−\sqrt{{x}^{\mathrm{2}} −\mathrm{4}} \\ $$$$\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}=\sqrt{{x}^{\mathrm{2}} −\mathrm{4}}+\mathrm{3} \\ $$$${x}^{\mathrm{2}} −\mathrm{3}=\mathrm{2}\sqrt{{x}^{\mathrm{2}} −\mathrm{4}} \\ $$$${x}^{\mathrm{4}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{9}=\mathrm{4}{x}^{\mathrm{2}} −\mathrm{16} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{5}\right)^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{5}\:\Rightarrow{x}=\pm\sqrt{\mathrm{5}} \\ $$
Commented by Tawa11 last updated on 17/Jul/22

$$\mathrm{Great}\:\mathrm{sirs} \\ $$
