
Question Number 45314 by mondodotto@gmail.com last updated on 11/Oct/18

$$\boldsymbol{\mathrm{solve}}\:\boldsymbol{\mathrm{for}}\:\boldsymbol{{x}} \\ $$$$\mathrm{10}^{\boldsymbol{{x}}} =\boldsymbol{{x}}^{\mathrm{50}} \\ $$
Answered by MrW3 last updated on 12/Oct/18
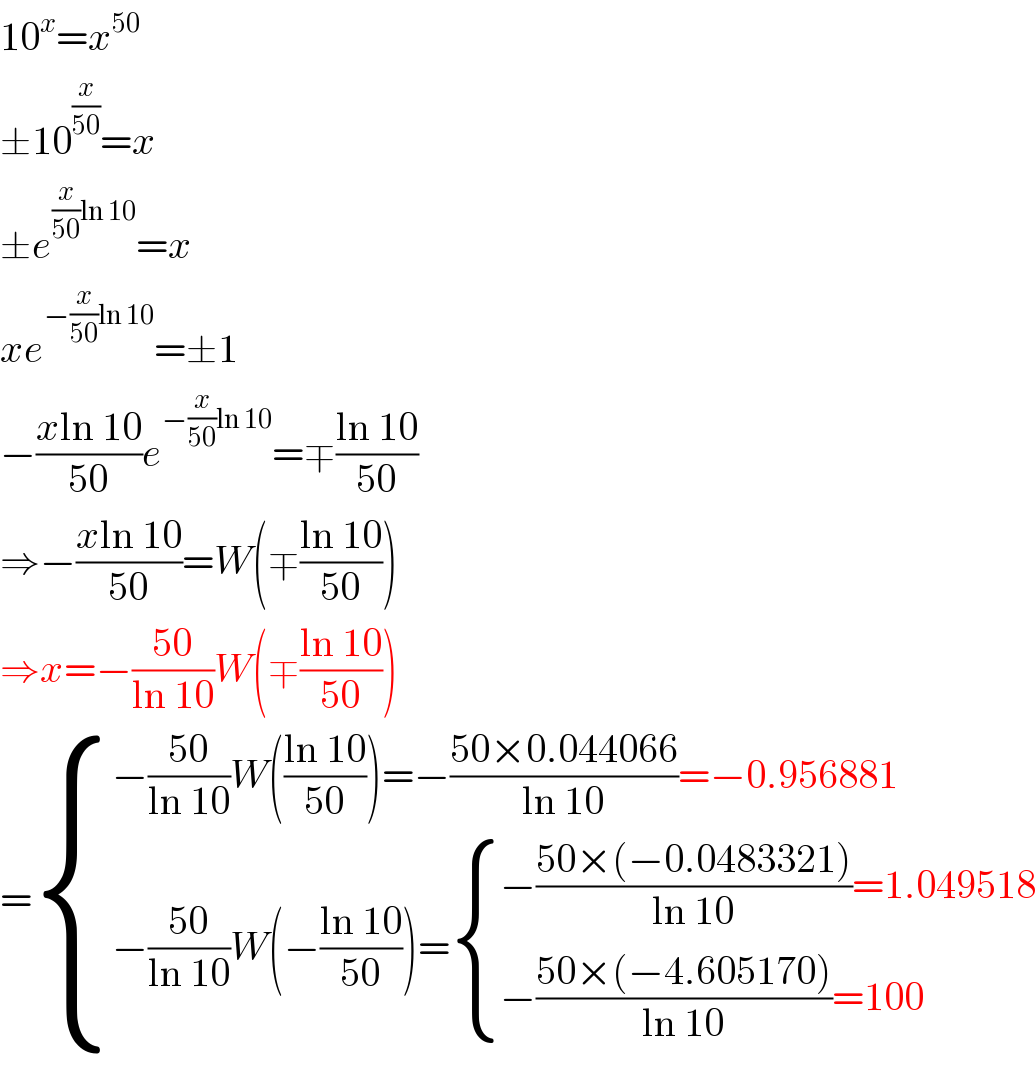
$$\mathrm{10}^{{x}} ={x}^{\mathrm{50}} \\ $$$$\pm\mathrm{10}^{\frac{{x}}{\mathrm{50}}} ={x} \\ $$$$\pm{e}^{\frac{{x}}{\mathrm{50}}\mathrm{ln}\:\mathrm{10}} ={x} \\ $$$${xe}^{−\frac{{x}}{\mathrm{50}}\mathrm{ln}\:\mathrm{10}} =\pm\mathrm{1} \\ $$$$−\frac{{x}\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}{e}^{−\frac{{x}}{\mathrm{50}}\mathrm{ln}\:\mathrm{10}} =\mp\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}} \\ $$$$\Rightarrow−\frac{{x}\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}={W}\left(\mp\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{50}}{\mathrm{ln}\:\mathrm{10}}{W}\left(\mp\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right) \\ $$$$=\begin{cases}{−\frac{\mathrm{50}}{\mathrm{ln}\:\mathrm{10}}{W}\left(\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right)=−\frac{\mathrm{50}×\mathrm{0}.\mathrm{044066}}{\mathrm{ln}\:\mathrm{10}}=−\mathrm{0}.\mathrm{956881}}\\{−\frac{\mathrm{50}}{\mathrm{ln}\:\mathrm{10}}{W}\left(−\frac{\mathrm{ln}\:\mathrm{10}}{\mathrm{50}}\right)=\begin{cases}{−\frac{\mathrm{50}×\left(−\mathrm{0}.\mathrm{0483321}\right)}{\mathrm{ln}\:\mathrm{10}}=\mathrm{1}.\mathrm{049518}}\\{−\frac{\mathrm{50}×\left(−\mathrm{4}.\mathrm{605170}\right)}{\mathrm{ln}\:\mathrm{10}}=\mathrm{100}}\end{cases}}\end{cases} \\ $$
Commented by mondodotto@gmail.com last updated on 12/Oct/18
$$\mathrm{thanx}\:\mathrm{atleast}\:\mathrm{i}\:\mathrm{get}\:\mathrm{something} \\ $$
Commented by mondodotto@gmail.com last updated on 12/Oct/18
$$\mathrm{thanx}\:\mathrm{a}\:\mathrm{lot}\:\mathrm{but}\:\mathrm{i}\:\mathrm{dont}\:\boldsymbol{\mathrm{undstnd}}\:\boldsymbol{\mathrm{this}}\:\boldsymbol{\mathrm{method}}\:\boldsymbol{\mathrm{please}}\:\boldsymbol{\mathrm{can}}\:\boldsymbol{\mathrm{you}}\:\boldsymbol{\mathrm{explain}}\:\boldsymbol{\mathrm{sir}} \\ $$
Commented by MrW3 last updated on 12/Oct/18
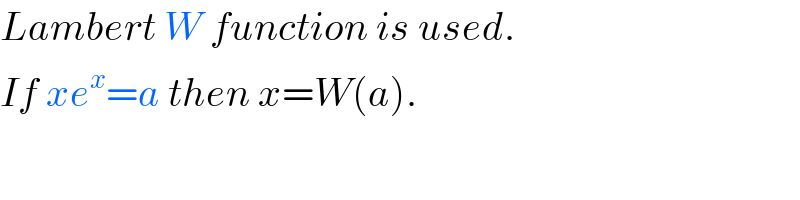
$${Lambert}\:{W}\:{function}\:{is}\:{used}. \\ $$$${If}\:{xe}^{{x}} ={a}\:{then}\:{x}={W}\left({a}\right). \\ $$
Commented by mondodotto@gmail.com last updated on 12/Oct/18

$$\mathrm{what}\:\mathrm{is}\:\boldsymbol{{W}} \\ $$
Commented by MrW3 last updated on 12/Oct/18

$${To}\:{apply}\:{Lambert}\:{function}\:{to}\:{solve} \\ $$$${the}\:{equation},\:{all}\:{what}\:{we}\:{have}\:{to}\:{do} \\ $$$${is}\:{to}\:{put}\:{the}\:{equation}\:{into}\:{a}\:{form}\:{like} \\ $$$${Xe}^{{X}} ={Y} \\ $$$${then}\:{we}\:{get}\:{X}=\mathbb{W}\left({Y}\right). \\ $$
Commented by MrW3 last updated on 12/Oct/18
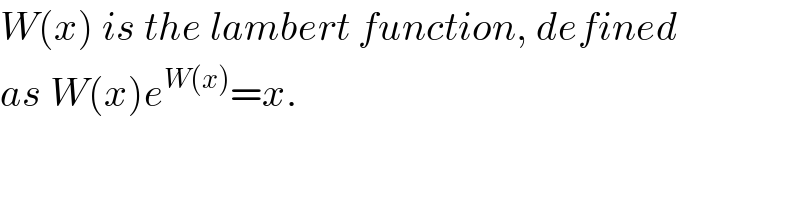
$${W}\left({x}\right)\:{is}\:{the}\:{lambert}\:{function},\:{defined} \\ $$$${as}\:{W}\left({x}\right){e}^{{W}\left({x}\right)} ={x}. \\ $$
