
Question Number 170520 by mr W last updated on 25/May/22
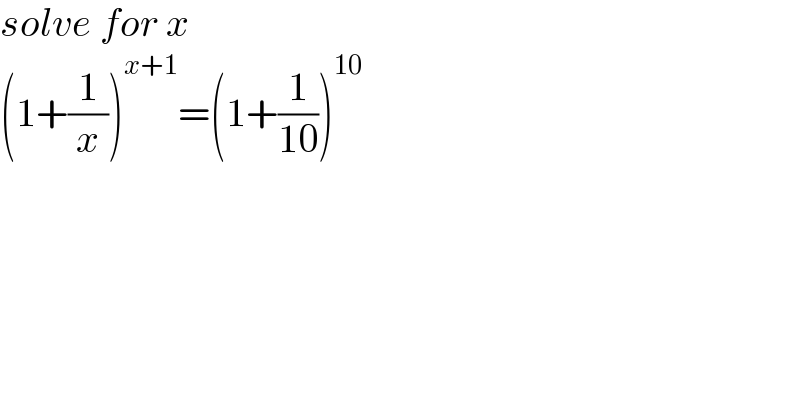
$${solve}\:{for}\:{x} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{x}}\right)^{{x}+\mathrm{1}} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}}\right)^{\mathrm{10}} \\ $$
Commented by mr W last updated on 26/May/22
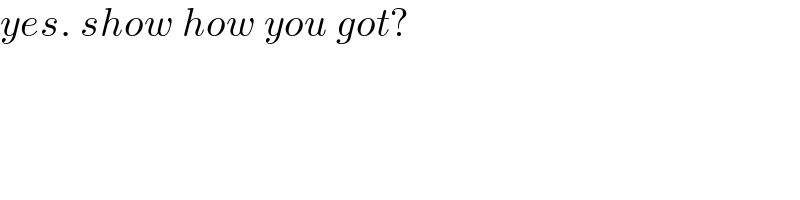
$${yes}.\:{show}\:{how}\:{you}\:{got}? \\ $$
Commented by cortano1 last updated on 25/May/22

$${x}=−\mathrm{11}\:? \\ $$
Answered by robertocaesar last updated on 26/May/22
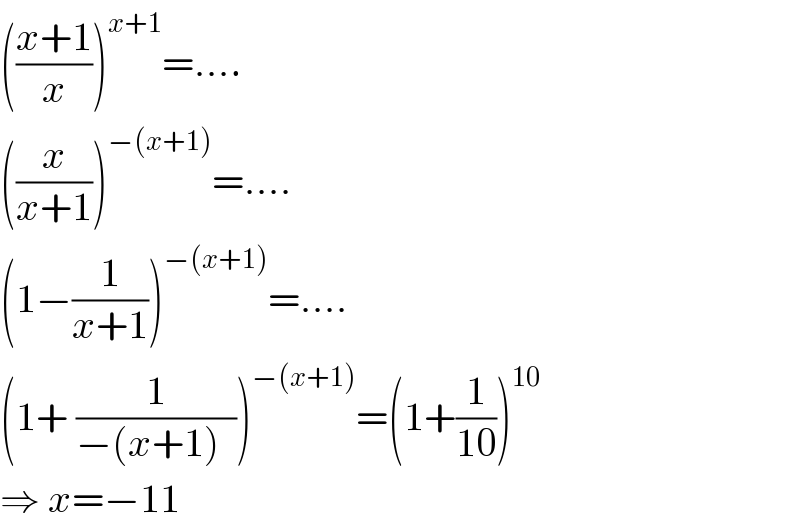
$$\left(\frac{{x}+\mathrm{1}}{{x}}\right)^{{x}+\mathrm{1}} =.... \\ $$$$\left(\frac{{x}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} =.... \\ $$$$\left(\mathrm{1}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)^{−\left({x}+\mathrm{1}\right)} =.... \\ $$$$\left(\mathrm{1}+\:\frac{\mathrm{1}}{−\left({x}+\mathrm{1}\right)\:\:}\right)^{−\left({x}+\mathrm{1}\right)} =\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{10}}\right)^{\mathrm{10}} \\ $$$$\Rightarrow\:{x}=−\mathrm{11} \\ $$
Commented by mr W last updated on 26/May/22

$${thanks}! \\ $$
