
Question Number 149240 by john_santu last updated on 04/Aug/21
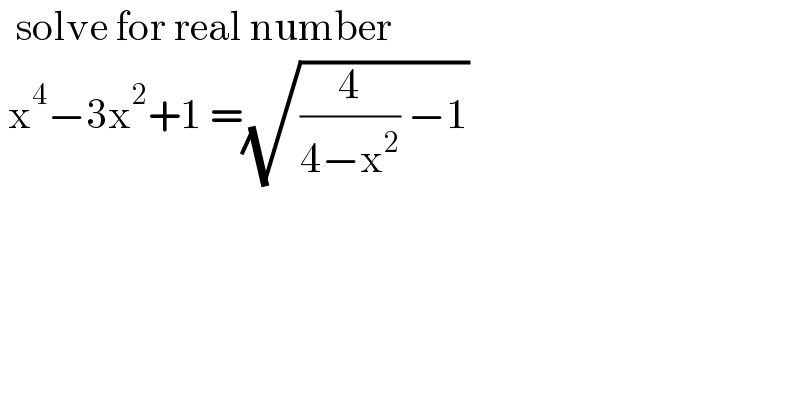
$$\:\:\mathrm{solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{number}\: \\ $$$$\:\mathrm{x}^{\mathrm{4}} −\mathrm{3x}^{\mathrm{2}} +\mathrm{1}\:=\sqrt{\frac{\mathrm{4}}{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }\:−\mathrm{1}} \\ $$$$\:\: \\ $$
Answered by MJS_new last updated on 04/Aug/21
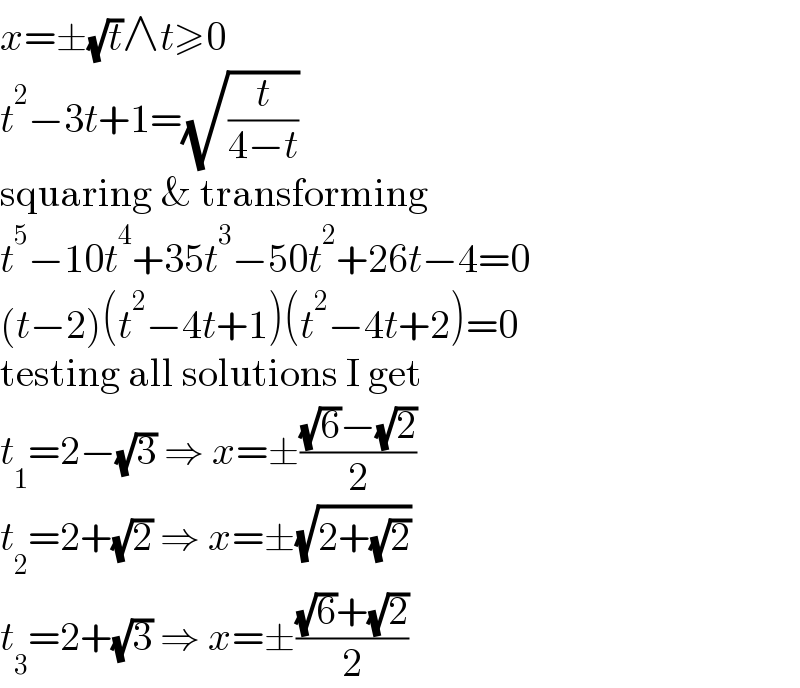
$${x}=\pm\sqrt{{t}}\wedge{t}\geqslant\mathrm{0} \\ $$$${t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}=\sqrt{\frac{{t}}{\mathrm{4}−{t}}} \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming} \\ $$$${t}^{\mathrm{5}} −\mathrm{10}{t}^{\mathrm{4}} +\mathrm{35}{t}^{\mathrm{3}} −\mathrm{50}{t}^{\mathrm{2}} +\mathrm{26}{t}−\mathrm{4}=\mathrm{0} \\ $$$$\left({t}−\mathrm{2}\right)\left({t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{1}\right)\left({t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\mathrm{testing}\:\mathrm{all}\:\mathrm{solutions}\:\mathrm{I}\:\mathrm{get} \\ $$$${t}_{\mathrm{1}} =\mathrm{2}−\sqrt{\mathrm{3}}\:\Rightarrow\:{x}=\pm\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${t}_{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{2}}\:\Rightarrow\:{x}=\pm\sqrt{\mathrm{2}+\sqrt{\mathrm{2}}} \\ $$$${t}_{\mathrm{3}} =\mathrm{2}+\sqrt{\mathrm{3}}\:\Rightarrow\:{x}=\pm\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$
Commented by john_santu last updated on 04/Aug/21
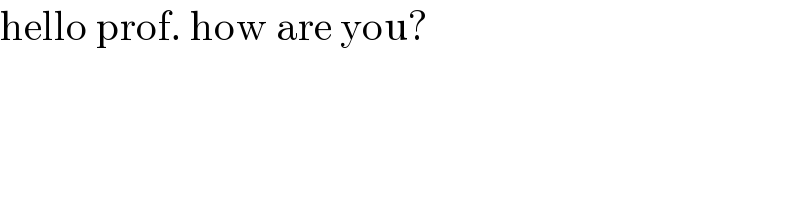
$$\mathrm{hello}\:\mathrm{prof}.\:\mathrm{how}\:\mathrm{are}\:\mathrm{you}? \\ $$
Commented by MJS_new last updated on 04/Aug/21
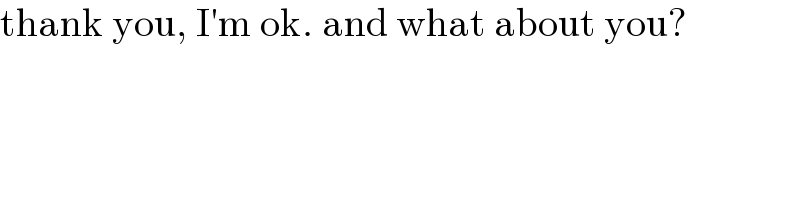
$$\mathrm{thank}\:\mathrm{you},\:\mathrm{I}'\mathrm{m}\:\mathrm{ok}.\:\mathrm{and}\:\mathrm{what}\:\mathrm{about}\:\mathrm{you}? \\ $$
Commented by john_santu last updated on 05/Aug/21

$$\mathrm{I}'\mathrm{m}\:\mathrm{ok}\:\mathrm{too}\:..\:\mathrm{prof} \\ $$
