
Previous in Differential Equation Next in Differential Equation
Question Number 16547 by Sai dadon. last updated on 23/Jun/17
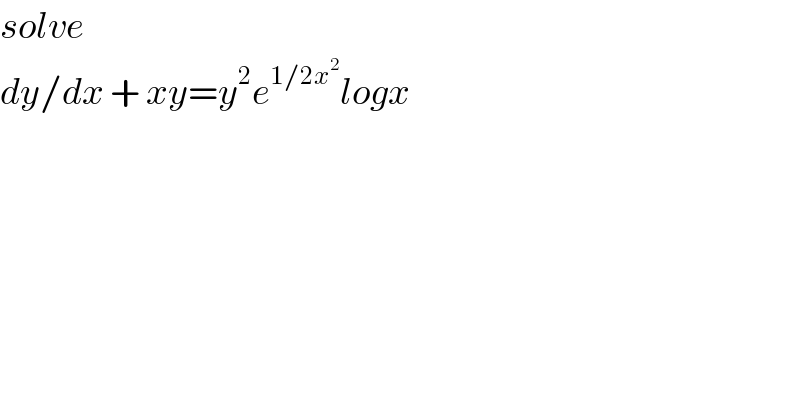
$${solve} \\ $$$${dy}/{dx}\:+\:{xy}={y}^{\mathrm{2}} {e}^{\mathrm{1}/\mathrm{2}{x}^{\mathrm{2}} } {logx} \\ $$
Commented by Sai dadon. last updated on 23/Jun/17

$${help} \\ $$
Commented by prakash jain last updated on 24/Jun/17
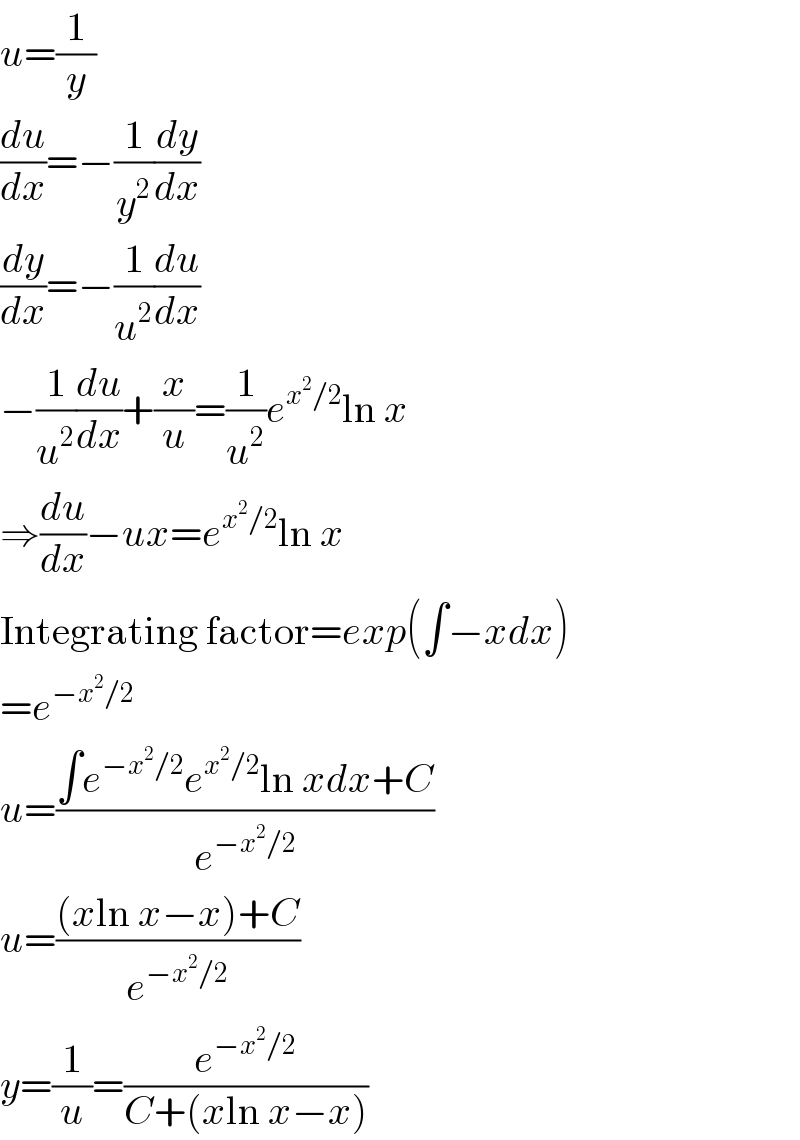
$${u}=\frac{\mathrm{1}}{{y}} \\ $$$$\frac{{du}}{{dx}}=−\frac{\mathrm{1}}{{y}^{\mathrm{2}} }\frac{{dy}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}=−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\frac{{du}}{{dx}} \\ $$$$−\frac{\mathrm{1}}{{u}^{\mathrm{2}} }\frac{{du}}{{dx}}+\frac{{x}}{{u}}=\frac{\mathrm{1}}{{u}^{\mathrm{2}} }{e}^{{x}^{\mathrm{2}} /\mathrm{2}} \mathrm{ln}\:{x} \\ $$$$\Rightarrow\frac{{du}}{{dx}}−{ux}={e}^{{x}^{\mathrm{2}} /\mathrm{2}} \mathrm{ln}\:{x} \\ $$$$\mathrm{Integrating}\:\mathrm{factor}={exp}\left(\int−{xdx}\right) \\ $$$$={e}^{−{x}^{\mathrm{2}} /\mathrm{2}} \\ $$$${u}=\frac{\int{e}^{−{x}^{\mathrm{2}} /\mathrm{2}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} \mathrm{ln}\:{xdx}+{C}}{{e}^{−{x}^{\mathrm{2}} /\mathrm{2}} } \\ $$$${u}=\frac{\left({x}\mathrm{ln}\:{x}−{x}\right)+{C}}{{e}^{−{x}^{\mathrm{2}} /\mathrm{2}} } \\ $$$${y}=\frac{\mathrm{1}}{{u}}=\frac{{e}^{−{x}^{\mathrm{2}} /\mathrm{2}} }{{C}+\left({x}\mathrm{ln}\:{x}−{x}\right)} \\ $$
Answered by prakash jain last updated on 24/Jun/17

$$\mathrm{Equations}\:\mathrm{of}\:\mathrm{form} \\ $$$$\frac{{dy}}{{dx}}+{yp}\left({x}\right)={y}^{{n}} {q}\left({x}\right) \\ $$$$\mathrm{are}\:\mathrm{called}\:\mathrm{Bernoulli}\:\mathrm{Equation} \\ $$$$\mathrm{and}\:\mathrm{can}\:\mathrm{be}\:\mathrm{solved}\:\mathrm{by}\:\mathrm{sunstituting} \\ $$$${u}={y}^{\mathrm{1}−{n}} \\ $$$$\mathrm{See}\:\mathrm{comment}\:\mathrm{for}\:\mathrm{solution}\:\mathrm{of} \\ $$$$\mathrm{above}\:\mathrm{equation} \\ $$
Commented by Sai dadon. last updated on 24/Jun/17

$${thanks}\:{sr} \\ $$
