
Previous in Differential Equation Next in Differential Equation
Question Number 117608 by TANMAY PANACEA last updated on 12/Oct/20

$${solve} \\ $$$$\frac{{d}^{\mathrm{2}} {y}}{{dt}^{\mathrm{2}} }+{w}^{\mathrm{2}} {x}=\mathrm{0} \\ $$
Answered by Dwaipayan Shikari last updated on 12/Oct/20
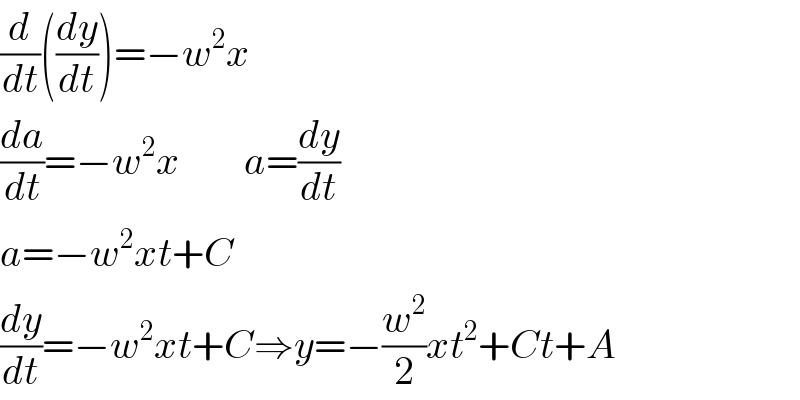
$$\frac{{d}}{{dt}}\left(\frac{{dy}}{{dt}}\right)=−{w}^{\mathrm{2}} {x} \\ $$$$\frac{{da}}{{dt}}=−{w}^{\mathrm{2}} {x}\:\:\:\:\:\:\:\:{a}=\frac{{dy}}{{dt}} \\ $$$${a}=−{w}^{\mathrm{2}} {xt}+{C} \\ $$$$\frac{{dy}}{{dt}}=−{w}^{\mathrm{2}} {xt}+{C}\Rightarrow{y}=−\frac{{w}^{\mathrm{2}} }{\mathrm{2}}{xt}^{\mathrm{2}} +{Ct}+{A} \\ $$
