Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 63945 by mathmax by abdo last updated on 11/Jul/19

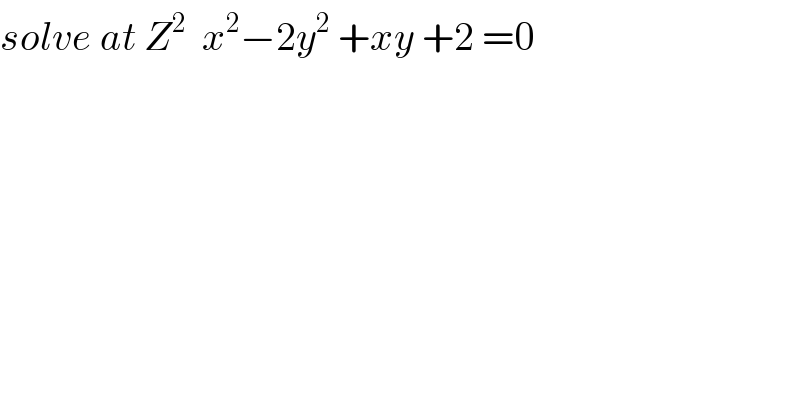
solve at Z^2 x^2 −2y^2 +xy +2 =0

$${solve}\:{at}\:{Z}^{\mathrm{2}} \:\:{x}^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} \:+{xy}\:+\mathrm{2}\:=\mathrm{0} \\ $$

Commented by hknkrc46 last updated on 11/Jul/19

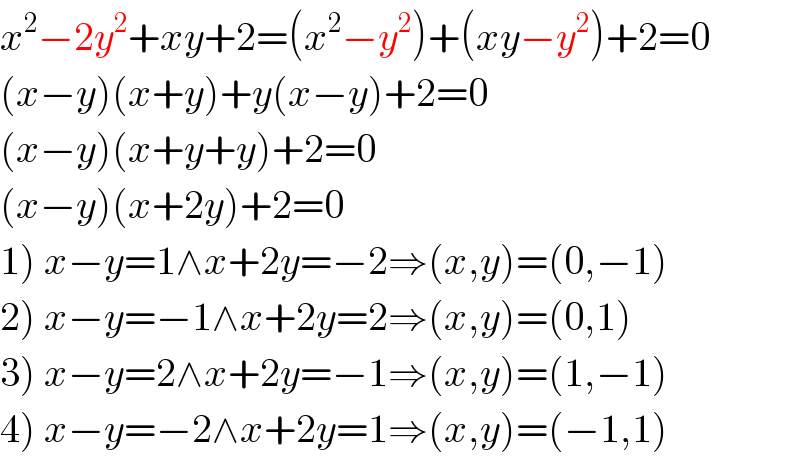
x^2 −2y^2 +xy+2=(x^2 −y^2 )+(xy−y^2 )+2=0 (x−y)(x+y)+y(x−y)+2=0 (x−y)(x+y+y)+2=0 (x−y)(x+2y)+2=0 1) x−y=1∧x+2y=−2⇒(x,y)=(0,−1) 2) x−y=−1∧x+2y=2⇒(x,y)=(0,1) 3) x−y=2∧x+2y=−1⇒(x,y)=(1,−1) 4) x−y=−2∧x+2y=1⇒(x,y)=(−1,1)

$${x}^{\mathrm{2}} −\mathrm{2}{y}^{\mathrm{2}} +{xy}+\mathrm{2}=\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} \right)+\left({xy}−{y}^{\mathrm{2}} \right)+\mathrm{2}=\mathrm{0} \\ $$$$\left({x}−{y}\right)\left({x}+{y}\right)+{y}\left({x}−{y}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\left({x}−{y}\right)\left({x}+{y}+{y}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\left({x}−{y}\right)\left({x}+\mathrm{2}{y}\right)+\mathrm{2}=\mathrm{0} \\ $$$$\left.\mathrm{1}\right)\:{x}−{y}=\mathrm{1}\wedge{x}+\mathrm{2}{y}=−\mathrm{2}\Rightarrow\left({x},{y}\right)=\left(\mathrm{0},−\mathrm{1}\right) \\ $$$$\left.\mathrm{2}\right)\:{x}−{y}=−\mathrm{1}\wedge{x}+\mathrm{2}{y}=\mathrm{2}\Rightarrow\left({x},{y}\right)=\left(\mathrm{0},\mathrm{1}\right) \\ $$$$\left.\mathrm{3}\right)\:{x}−{y}=\mathrm{2}\wedge{x}+\mathrm{2}{y}=−\mathrm{1}\Rightarrow\left({x},{y}\right)=\left(\mathrm{1},−\mathrm{1}\right) \\ $$$$\left.\mathrm{4}\right)\:{x}−{y}=−\mathrm{2}\wedge{x}+\mathrm{2}{y}=\mathrm{1}\Rightarrow\left({x},{y}\right)=\left(−\mathrm{1},\mathrm{1}\right) \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com