
Question Number 196652 by SANOGO last updated on 28/Aug/23
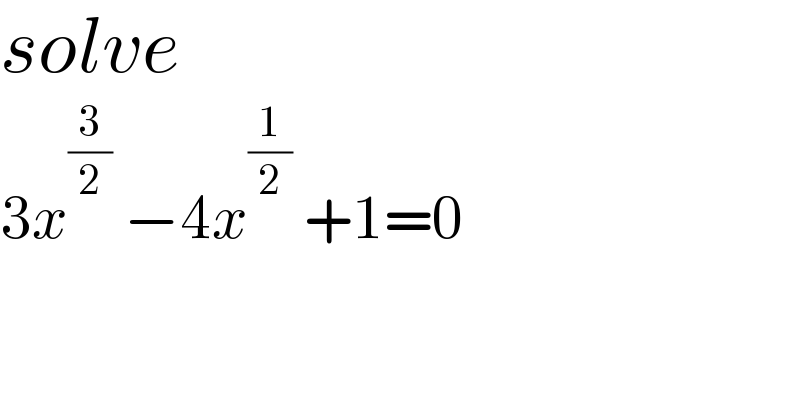
$${solve} \\ $$$$\mathrm{3}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \:−\mathrm{4}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} \:+\mathrm{1}=\mathrm{0} \\ $$
Answered by BaliramKumar last updated on 28/Aug/23
![3((√x))^3 − 3(√x) −(√x) +1 = 0 3(√x)[((√x))^2 −1] −( (√x) −1)= 0 3(√x)[((√x)−1)((√x) +1)] −( (√x) −1)= 0 ((√x)−1)[3((√x))^2 +3(√x) − 1]= 0 (√x) − 1 = 0 or 3((√x))^2 + 3(√x) − 1 =0 (√x) = 1 (√x) = ((−3 ± (√(21)))/6) x = 1 (√x) = ((−3 +(√(21)))/6) or (√x) = ((−3 − (√(21)))/6) (√x) = (√(((−3 + (√(21)))^2 )/(36))) invalid (√x) = (√(((30 − 6(√(21))))/(36))) (√x) = (√((5 − (√(21)))/6)) x = ((5 − (√(21)))/6)](Q196654.png)
$$ \\ $$$$\mathrm{3}\left(\sqrt{{x}}\right)^{\mathrm{3}} \:−\:\mathrm{3}\sqrt{{x}}\:−\sqrt{{x}}\:+\mathrm{1}\:=\:\mathrm{0} \\ $$$$\mathrm{3}\sqrt{{x}}\left[\left(\sqrt{{x}}\right)^{\mathrm{2}} −\mathrm{1}\right]\:−\left(\:\sqrt{{x}}\:−\mathrm{1}\right)=\:\mathrm{0} \\ $$$$\mathrm{3}\sqrt{{x}}\left[\left(\sqrt{{x}}−\mathrm{1}\right)\left(\sqrt{{x}}\:+\mathrm{1}\right)\right]\:−\left(\:\sqrt{{x}}\:−\mathrm{1}\right)=\:\mathrm{0} \\ $$$$\left(\sqrt{{x}}−\mathrm{1}\right)\left[\mathrm{3}\left(\sqrt{{x}}\right)^{\mathrm{2}} \:+\mathrm{3}\sqrt{{x}}\:−\:\mathrm{1}\right]=\:\mathrm{0} \\ $$$$\sqrt{{x}}\:−\:\mathrm{1}\:=\:\mathrm{0}\:{or}\:\mathrm{3}\left(\sqrt{{x}}\right)^{\mathrm{2}} \:+\:\mathrm{3}\sqrt{{x}}\:−\:\mathrm{1}\:=\mathrm{0} \\ $$$$\sqrt{{x}}\:=\:\mathrm{1}\:\:\:\:\:\:\:\:\:\sqrt{{x}}\:=\:\frac{−\mathrm{3}\:\pm\:\sqrt{\mathrm{21}}}{\mathrm{6}} \\ $$$${x}\:=\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\sqrt{{x}}\:=\:\frac{−\mathrm{3}\:+\sqrt{\mathrm{21}}}{\mathrm{6}}\:{or}\:\sqrt{{x}}\:=\:\frac{−\mathrm{3}\:−\:\sqrt{\mathrm{21}}}{\mathrm{6}} \\ $$$$\sqrt{{x}}\:=\:\sqrt{\frac{\left(−\mathrm{3}\:+\:\sqrt{\mathrm{21}}\right)^{\mathrm{2}} }{\mathrm{36}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{invalid} \\ $$$$\sqrt{{x}}\:=\:\sqrt{\frac{\left(\mathrm{30}\:−\:\mathrm{6}\sqrt{\mathrm{21}}\right)}{\mathrm{36}}}\: \\ $$$$\sqrt{{x}}\:=\:\sqrt{\frac{\mathrm{5}\:−\:\sqrt{\mathrm{21}}}{\mathrm{6}}}\: \\ $$$${x}\:=\:\frac{\mathrm{5}\:−\:\sqrt{\mathrm{21}}}{\mathrm{6}}\: \\ $$$$ \\ $$
Answered by Frix last updated on 28/Aug/23
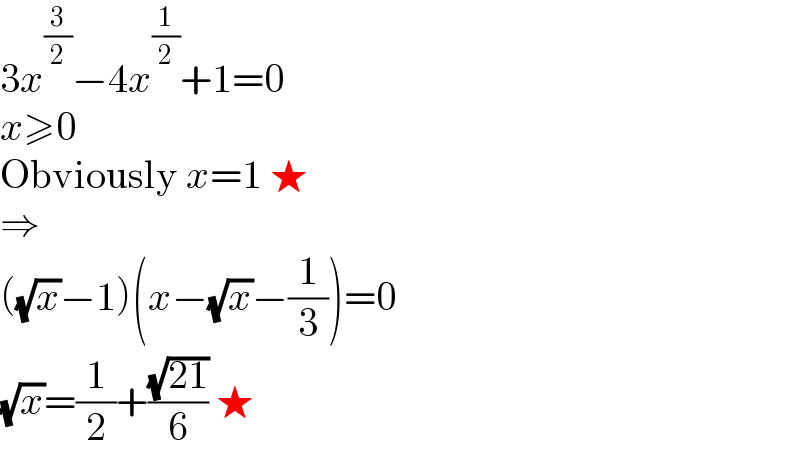
$$\mathrm{3}{x}^{\frac{\mathrm{3}}{\mathrm{2}}} −\mathrm{4}{x}^{\frac{\mathrm{1}}{\mathrm{2}}} +\mathrm{1}=\mathrm{0} \\ $$$${x}\geqslant\mathrm{0} \\ $$$$\mathrm{Obviously}\:{x}=\mathrm{1}\:\bigstar \\ $$$$\Rightarrow \\ $$$$\left(\sqrt{{x}}−\mathrm{1}\right)\left({x}−\sqrt{{x}}−\frac{\mathrm{1}}{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\sqrt{{x}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{21}}}{\mathrm{6}}\:\bigstar \\ $$
