
Question Number 27976 by NECx last updated on 18/Jan/18
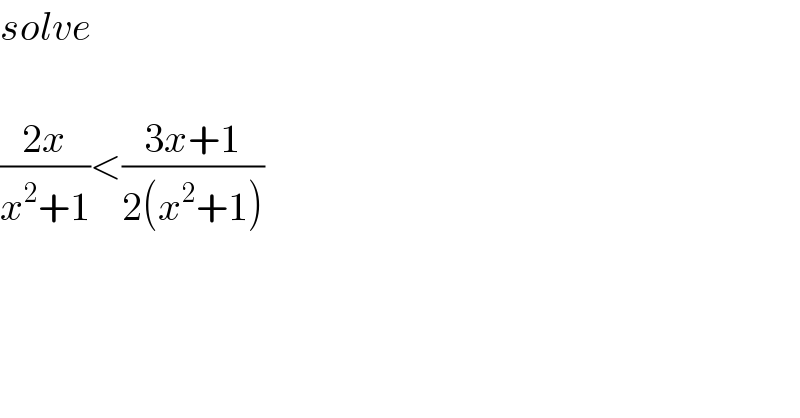
$${solve} \\ $$ $$ \\ $$ $$\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}<\frac{\mathrm{3}{x}+\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)} \\ $$ $$ \\ $$
Commented byabdo imad last updated on 18/Jan/18
![due to x^2 +1>0 ( e) ⇔ 2x < ((3x+1)/2) ⇔ 4x −3x−1<0 ⇔ x−1<0 ⇔ x <1 ⇔ x∈ ]−∝ ,1[](Q28032.png)
$${due}\:{to}\:\:\:{x}^{\mathrm{2}} +\mathrm{1}>\mathrm{0}\:\:\:\left(\:{e}\right)\:\:\Leftrightarrow\:\:\:\mathrm{2}{x}\:<\:\:\:\frac{\mathrm{3}{x}+\mathrm{1}}{\mathrm{2}} \\ $$ $$\left.\Leftrightarrow\:\:\mathrm{4}{x}\:−\mathrm{3}{x}−\mathrm{1}<\mathrm{0}\:\Leftrightarrow\:\:{x}−\mathrm{1}<\mathrm{0}\:\:\Leftrightarrow\:\:{x}\:<\mathrm{1}\:\:\:\Leftrightarrow\:{x}\in\:\right]−\propto\:,\mathrm{1}\left[\right. \\ $$
Answered by Rasheed.Sindhi last updated on 18/Jan/18
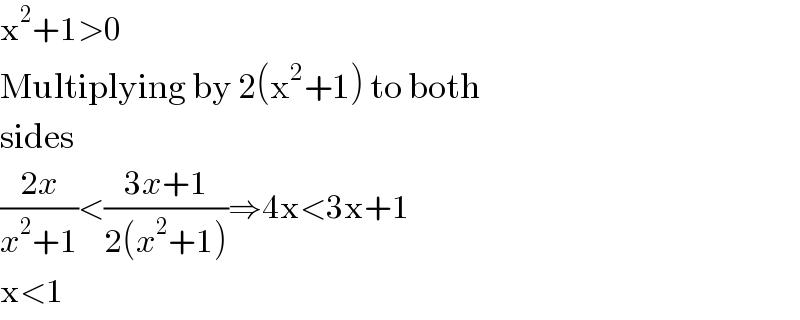
$$\mathrm{x}^{\mathrm{2}} +\mathrm{1}>\mathrm{0} \\ $$ $$\mathrm{Multiplying}\:\mathrm{by}\:\mathrm{2}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{1}\right)\:\mathrm{to}\:\mathrm{both} \\ $$ $$\mathrm{sides} \\ $$ $$\frac{\mathrm{2}{x}}{{x}^{\mathrm{2}} +\mathrm{1}}<\frac{\mathrm{3}{x}+\mathrm{1}}{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{1}\right)}\Rightarrow\mathrm{4x}<\mathrm{3x}+\mathrm{1} \\ $$ $$\mathrm{x}<\mathrm{1} \\ $$
