
Question Number 171771 by Mikenice last updated on 20/Jun/22
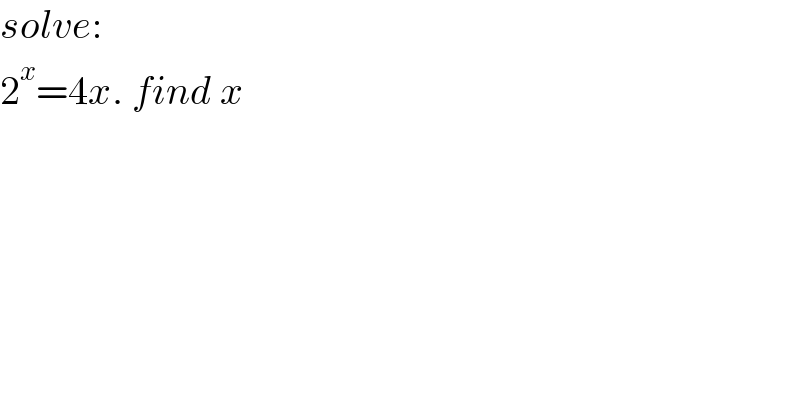
$${solve}: \\ $$$$\mathrm{2}^{{x}} =\mathrm{4}{x}.\:{find}\:{x} \\ $$
Answered by mathocean1 last updated on 20/Jun/22

$${S}_{\mathbb{R}} =\left\{\mathrm{4}\right\} \\ $$
Answered by mr W last updated on 20/Jun/22
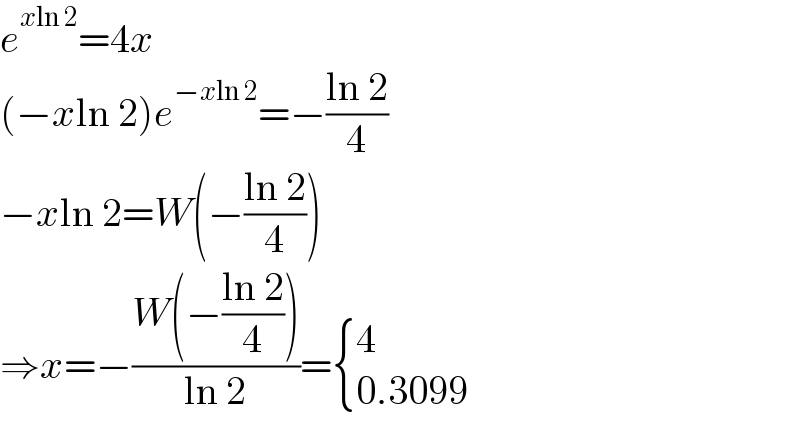
$${e}^{{x}\mathrm{ln}\:\mathrm{2}} =\mathrm{4}{x} \\ $$$$\left(−{x}\mathrm{ln}\:\mathrm{2}\right){e}^{−{x}\mathrm{ln}\:\mathrm{2}} =−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}} \\ $$$$−{x}\mathrm{ln}\:\mathrm{2}={W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right) \\ $$$$\Rightarrow{x}=−\frac{{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right)}{\mathrm{ln}\:\mathrm{2}}=\begin{cases}{\mathrm{4}}\\{\mathrm{0}.\mathrm{3099}}\end{cases} \\ $$
Commented by daus last updated on 21/Jun/22
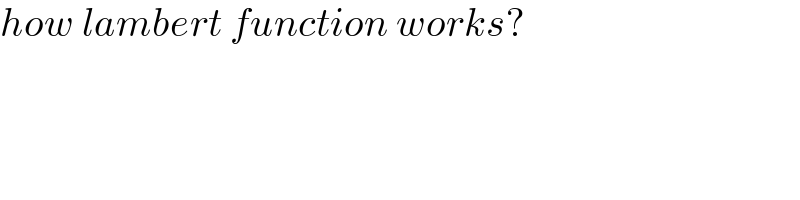
$${how}\:{lambert}\:{function}\:{works}? \\ $$
Commented by mr W last updated on 21/Jun/22
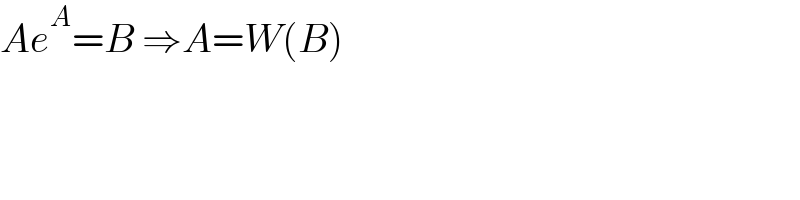
$${Ae}^{{A}} ={B}\:\Rightarrow{A}={W}\left({B}\right) \\ $$
