
Question Number 172111 by Mikenice last updated on 23/Jun/22

$${solve} \\ $$$$\mathrm{2}^{{x}} =\mathrm{4}{x} \\ $$
Commented by mr W last updated on 23/Jun/22
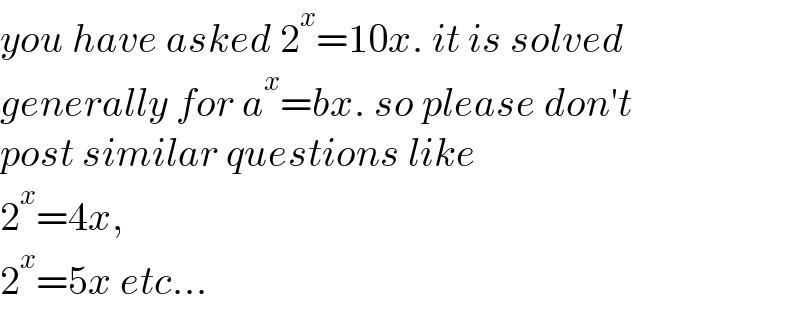
$${you}\:{have}\:{asked}\:\mathrm{2}^{{x}} =\mathrm{10}{x}.\:{it}\:{is}\:{solved} \\ $$$${generally}\:{for}\:{a}^{{x}} ={bx}.\:{so}\:{please}\:{don}'{t}\: \\ $$$${post}\:{similar}\:{questions}\:{like} \\ $$$$\mathrm{2}^{{x}} =\mathrm{4}{x},\: \\ $$$$\mathrm{2}^{{x}} =\mathrm{5}{x}\:{etc}... \\ $$
Answered by Mikenice last updated on 23/Jun/22
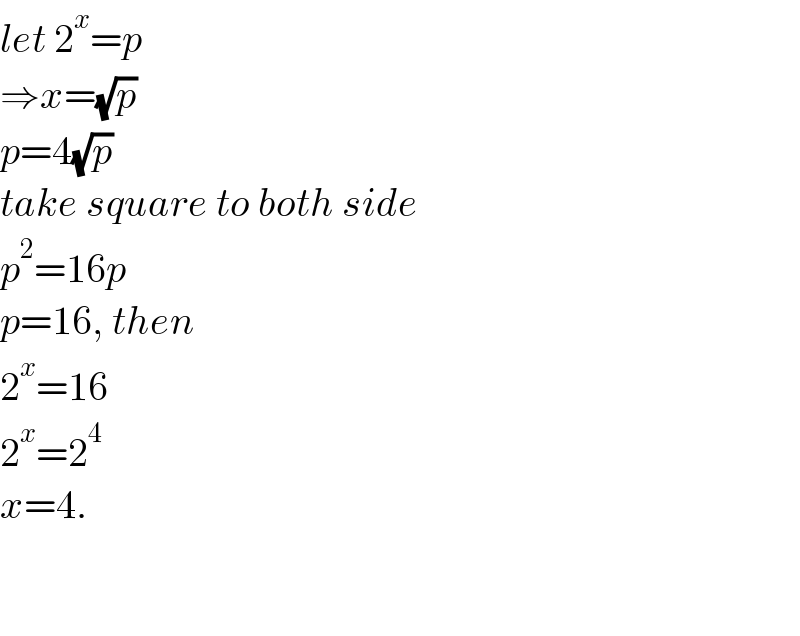
$${let}\:\mathrm{2}^{{x}} ={p} \\ $$$$\Rightarrow{x}=\sqrt{{p}} \\ $$$${p}=\mathrm{4}\sqrt{{p}} \\ $$$${take}\:{square}\:{to}\:{both}\:{side} \\ $$$${p}^{\mathrm{2}} =\mathrm{16}{p} \\ $$$${p}=\mathrm{16},\:{then} \\ $$$$\mathrm{2}^{{x}} =\mathrm{16} \\ $$$$\mathrm{2}^{{x}} =\mathrm{2}^{\mathrm{4}} \\ $$$${x}=\mathrm{4}. \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 23/Jun/22
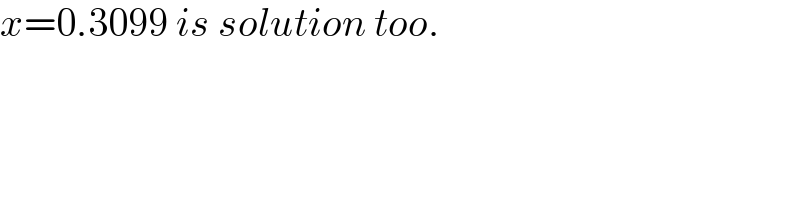
$${x}=\mathrm{0}.\mathrm{3099}\:{is}\:{solution}\:{too}. \\ $$
Commented by mr W last updated on 23/Jun/22
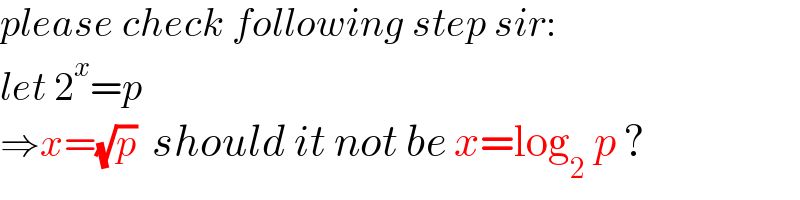
$${please}\:{check}\:{following}\:{step}\:{sir}: \\ $$$${let}\:\mathrm{2}^{{x}} ={p} \\ $$$$\Rightarrow{x}=\sqrt{{p}}\:\:{should}\:{it}\:{not}\:{be}\:{x}=\mathrm{log}_{\mathrm{2}} \:{p}\:? \\ $$
Commented by Mikenice last updated on 23/Jun/22
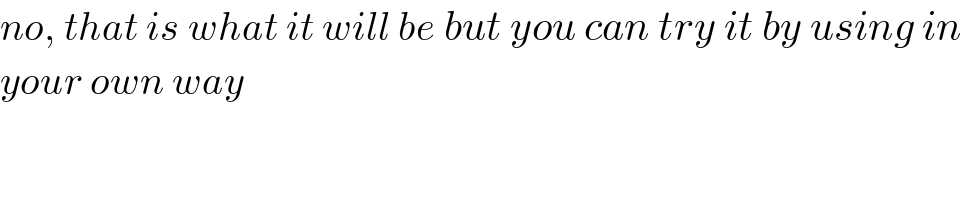
$${no},\:{that}\:{is}\:{what}\:{it}\:{will}\:{be}\:{but}\:{you}\:{can}\:{try}\:{it}\:{by}\:{using}\:{in}\: \\ $$$${your}\:{own}\:{way} \\ $$
Commented by mr W last updated on 24/Jun/22

$$\mathrm{2}^{{x}} ={p}\:\Rightarrow{x}=\sqrt{{p}}\:{is}\:{wrong}.\: \\ $$$${not}\:{i}\:{say}\:{that},\:{but}\:{the}\:{mathematics}\: \\ $$$${says}\:{that}.\: \\ $$$${IT}\:{IS}\:{NOT}\:{PERSONAL}\:{sir}. \\ $$
Answered by Mikenice last updated on 24/Jun/22
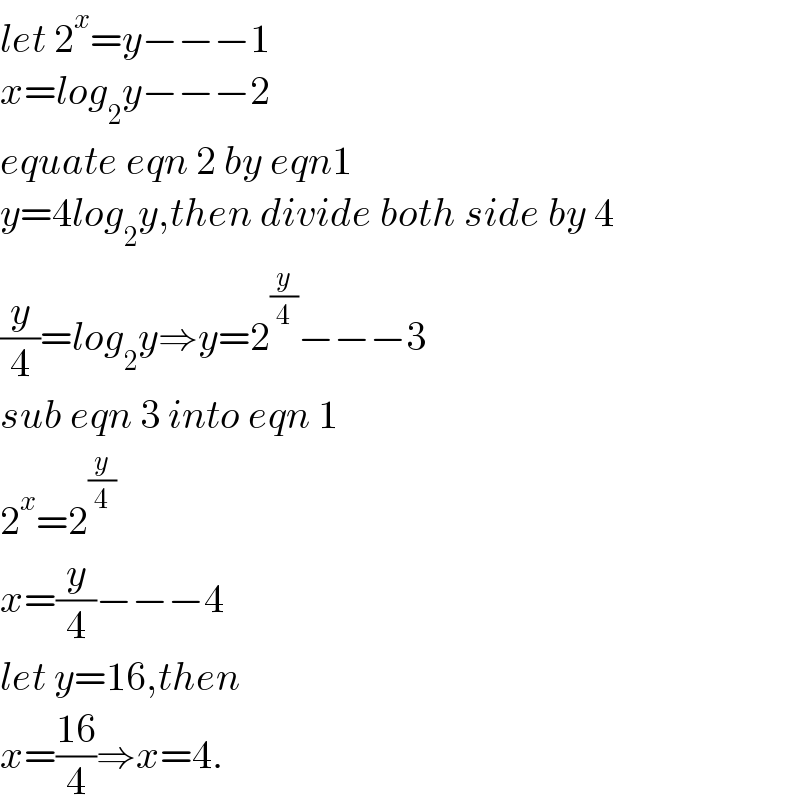
$${let}\:\mathrm{2}^{{x}} ={y}−−−\mathrm{1} \\ $$$${x}={log}_{\mathrm{2}} {y}−−−\mathrm{2} \\ $$$${equate}\:{eqn}\:\mathrm{2}\:{by}\:{eqn}\mathrm{1} \\ $$$${y}=\mathrm{4}{log}_{\mathrm{2}} {y},{then}\:{divide}\:{both}\:{side}\:{by}\:\mathrm{4} \\ $$$$\frac{{y}}{\mathrm{4}}={log}_{\mathrm{2}} {y}\Rightarrow{y}=\mathrm{2}^{\frac{{y}}{\mathrm{4}}} −−−\mathrm{3} \\ $$$${sub}\:{eqn}\:\mathrm{3}\:{into}\:{eqn}\:\mathrm{1} \\ $$$$\mathrm{2}^{{x}} =\mathrm{2}^{\frac{{y}}{\mathrm{4}}} \\ $$$${x}=\frac{{y}}{\mathrm{4}}−−−\mathrm{4} \\ $$$${let}\:{y}=\mathrm{16},{then} \\ $$$${x}=\frac{\mathrm{16}}{\mathrm{4}}\Rightarrow{x}=\mathrm{4}. \\ $$
Answered by mr W last updated on 25/Jun/22

$$\mathrm{2}^{{x}} =\mathrm{4}{x} \\ $$$${e}^{{x}\mathrm{ln}\:\mathrm{2}} =\mathrm{4}{x} \\ $$$$\left(−{x}\mathrm{ln}\:\mathrm{2}\right){e}^{−{x}\mathrm{ln}\:\mathrm{2}} =−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}} \\ $$$$−{x}\mathrm{ln}\:\mathrm{2}={W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right) \\ $$$$\Rightarrow{x}=−\frac{{W}\left(−\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{4}}\right)}{\mathrm{ln}\:\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:=\begin{cases}{−\frac{−\mathrm{2}.\mathrm{77258872}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{4}}\\{−\frac{−\mathrm{0}.\mathrm{21481112}}{\mathrm{ln}\:\mathrm{2}}=\mathrm{0}.\mathrm{309907}}\end{cases} \\ $$$$ \\ $$$${generally}\:{for} \\ $$$$\boldsymbol{{a}}^{\boldsymbol{{x}}} =\boldsymbol{{bx}} \\ $$$$\Rightarrow\boldsymbol{{x}}=−\frac{\boldsymbol{{W}}\left(−\frac{\boldsymbol{\mathrm{ln}}\:\boldsymbol{{a}}}{\boldsymbol{{b}}}\right)}{\boldsymbol{\mathrm{ln}}\:\boldsymbol{{a}}} \\ $$
