
Question Number 172086 by Mikenice last updated on 23/Jun/22

$${solve} \\ $$$$\mathrm{2}^{{x}^{\mathrm{2}} } −\mathrm{40}{x}=\mathrm{0} \\ $$
Commented by mr W last updated on 23/Jun/22
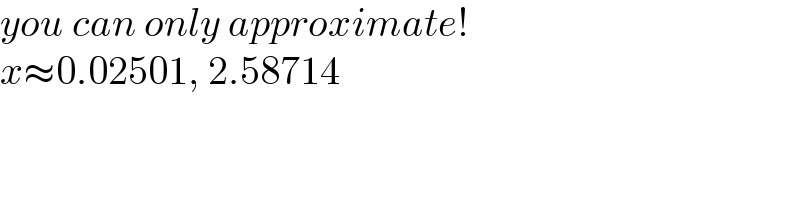
$${you}\:{can}\:{only}\:{approximate}! \\ $$$${x}\approx\mathrm{0}.\mathrm{02501},\:\mathrm{2}.\mathrm{58714} \\ $$
Commented by Mikenice last updated on 23/Jun/22
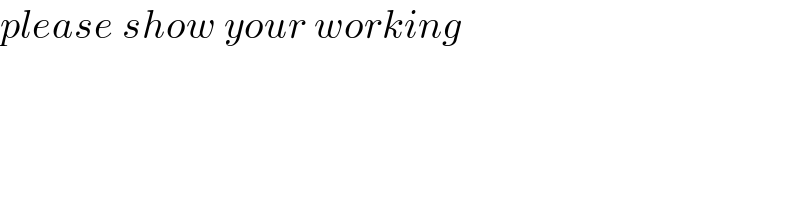
$${please}\:{show}\:{your}\:{working} \\ $$
Commented by nanakay_jp last updated on 23/Jun/22
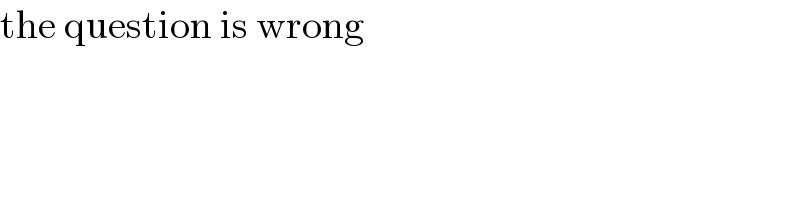
$$\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{wrong} \\ $$
Commented by mr W last updated on 23/Jun/22
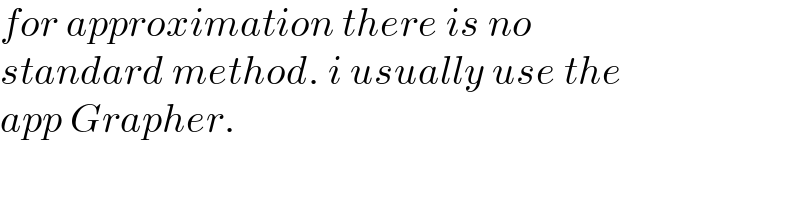
$${for}\:{approximation}\:{there}\:{is}\:{no}\: \\ $$$${standard}\:{method}.\:{i}\:{usually}\:{use}\:{the} \\ $$$${app}\:{Grapher}. \\ $$
Commented by mr W last updated on 24/Jun/22
$${i}\:{found}\:{a}\:{way}\:{for}\:{exact}\:{solution},\: \\ $$$${see}\:{Q}\mathrm{172244}. \\ $$
Answered by nanakay_jp last updated on 23/Jun/22

Commented by mr W last updated on 23/Jun/22

$${wrong}! \\ $$$$\mathrm{2}^{{x}^{\mathrm{2}} } \neq\mathrm{2}{x}^{\mathrm{2}} \\ $$
