
Question Number 167473 by mnjuly1970 last updated on 17/Mar/22
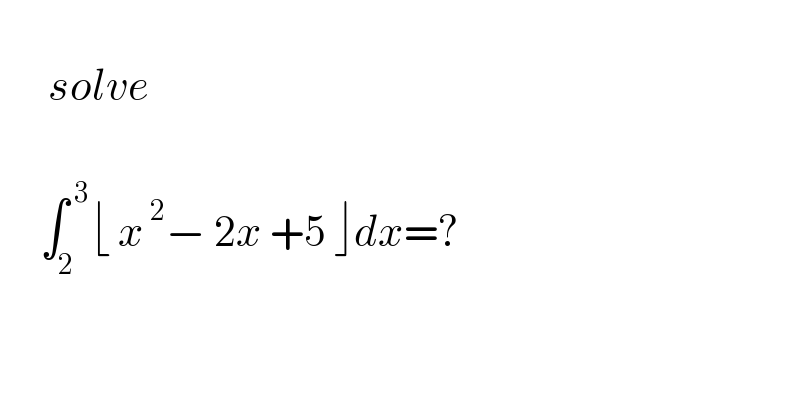
$$\:\: \\ $$$$\:\:\:\:\:\:{solve} \\ $$$$ \\ $$$$\:\:\:\:\:\int_{\mathrm{2}} ^{\:\mathrm{3}} \lfloor\:{x}^{\:\mathrm{2}} −\:\mathrm{2}{x}\:+\mathrm{5}\:\rfloor{dx}=? \\ $$$$ \\ $$
Answered by MJS_new last updated on 17/Mar/22
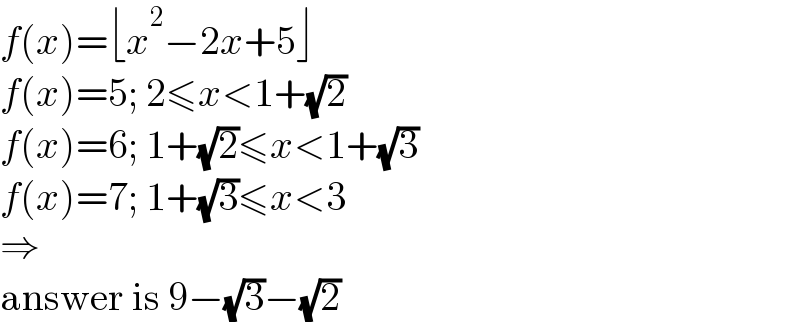
$${f}\left({x}\right)=\lfloor{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{5}\rfloor \\ $$$${f}\left({x}\right)=\mathrm{5};\:\mathrm{2}\leqslant{x}<\mathrm{1}+\sqrt{\mathrm{2}} \\ $$$${f}\left({x}\right)=\mathrm{6};\:\mathrm{1}+\sqrt{\mathrm{2}}\leqslant{x}<\mathrm{1}+\sqrt{\mathrm{3}} \\ $$$${f}\left({x}\right)=\mathrm{7};\:\mathrm{1}+\sqrt{\mathrm{3}}\leqslant{x}<\mathrm{3} \\ $$$$\Rightarrow \\ $$$$\mathrm{answer}\:\mathrm{is}\:\mathrm{9}−\sqrt{\mathrm{3}}−\sqrt{\mathrm{2}} \\ $$
Commented by mnjuly1970 last updated on 17/Mar/22

$${grateful}\: \\ $$
Answered by mathman1234 last updated on 17/Mar/22
![∫_2 ^3 (x^2 −2x+5)dx= [(x^3 /3) −x^2 +5x]_2 ^3 = (9−9+15)−((8/3)−4+10) = ((19)/3)](Q167481.png)
$$\:\:\:\:\int_{\mathrm{2}} ^{\mathrm{3}} \left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{5}\right)\mathrm{dx}=\:\left[\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{3}}\:−\mathrm{x}^{\mathrm{2}} +\mathrm{5x}\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\left(\mathrm{9}−\mathrm{9}+\mathrm{15}\right)−\left(\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{4}+\mathrm{10}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{19}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 17/Mar/22
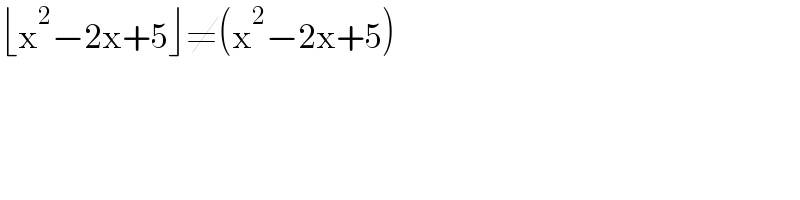
$$\lfloor\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{5}\rfloor\neq\left(\mathrm{x}^{\mathrm{2}} −\mathrm{2x}+\mathrm{5}\right) \\ $$
Commented by mnjuly1970 last updated on 18/Mar/22

$$\checkmark \\ $$
