Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 180785 by Vynho last updated on 17/Nov/22

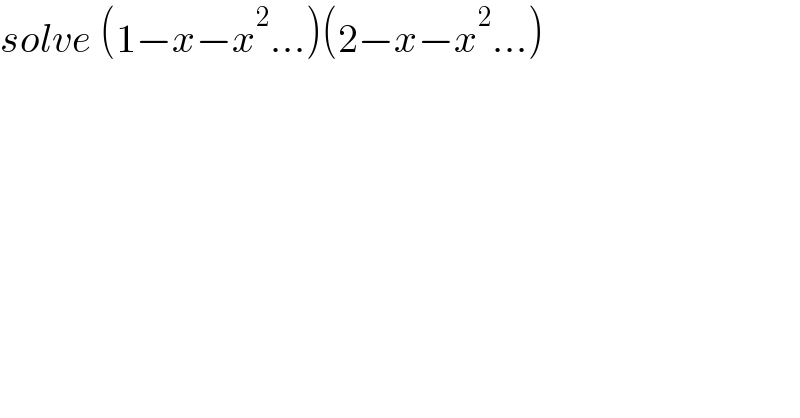
solve (1−x−x^2 ...)(2−x−x^2 ...)

$${solve}\:\left(\mathrm{1}−{x}−{x}^{\mathrm{2}} ...\right)\left(\mathrm{2}−{x}−{x}^{\mathrm{2}} ...\right) \\ $$

Answered by Rasheed.Sindhi last updated on 17/Nov/22

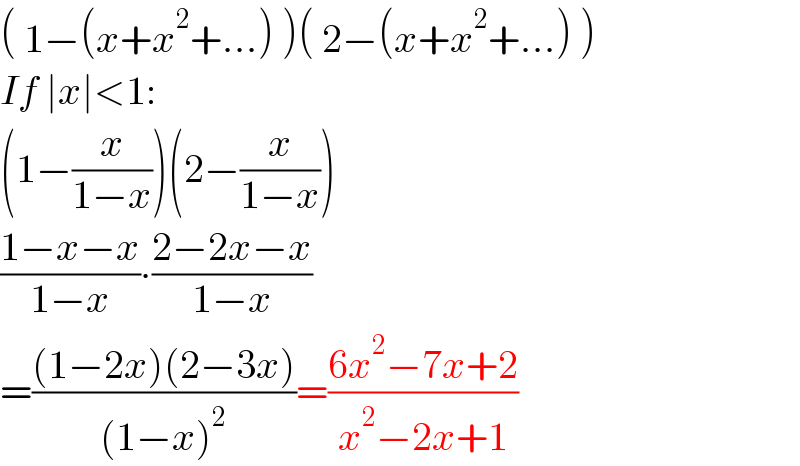
( 1−(x+x^2 +...) )( 2−(x+x^2 +...) ) If ∣x∣<1: (1−(x/(1−x)))(2−(x/(1−x))) ((1−x−x)/(1−x))∙((2−2x−x)/(1−x)) =(((1−2x)(2−3x))/((1−x)^2 ))=((6x^2 −7x+2)/(x^2 −2x+1))

$$\left(\:\mathrm{1}−\left({x}+{x}^{\mathrm{2}} +...\right)\:\right)\left(\:\mathrm{2}−\left({x}+{x}^{\mathrm{2}} +...\right)\:\right) \\ $$$${If}\:\mid{x}\mid<\mathrm{1}: \\ $$$$\left(\mathrm{1}−\frac{{x}}{\mathrm{1}−{x}}\right)\left(\mathrm{2}−\frac{{x}}{\mathrm{1}−{x}}\right) \\ $$$$\frac{\mathrm{1}−{x}−{x}}{\mathrm{1}−{x}}\centerdot\frac{\mathrm{2}−\mathrm{2}{x}−{x}}{\mathrm{1}−{x}} \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{2}{x}\right)\left(\mathrm{2}−\mathrm{3}{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }=\frac{\mathrm{6}{x}^{\mathrm{2}} −\mathrm{7}{x}+\mathrm{2}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{1}} \\ $$

Answered by mr W last updated on 17/Nov/22

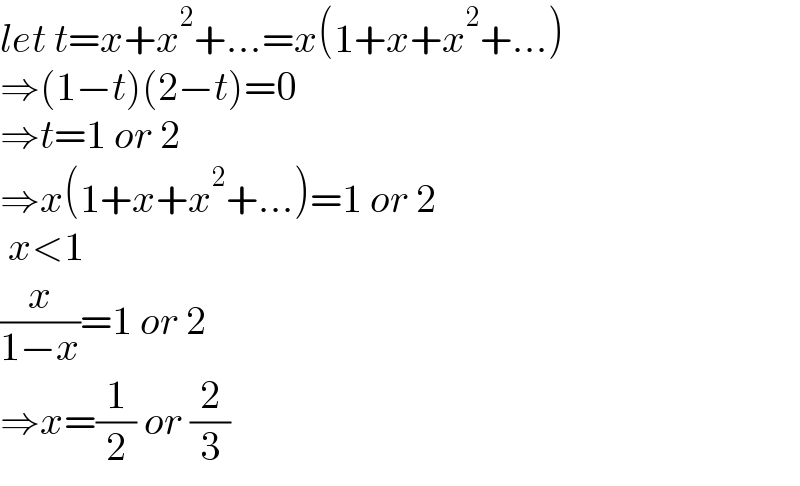
let t=x+x^2 +...=x(1+x+x^2 +...) ⇒(1−t)(2−t)=0 ⇒t=1 or 2 ⇒x(1+x+x^2 +...)=1 or 2 x<1 (x/(1−x))=1 or 2 ⇒x=(1/2) or (2/3)

$${let}\:{t}={x}+{x}^{\mathrm{2}} +...={x}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +...\right) \\ $$$$\Rightarrow\left(\mathrm{1}−{t}\right)\left(\mathrm{2}−{t}\right)=\mathrm{0} \\ $$$$\Rightarrow{t}=\mathrm{1}\:{or}\:\mathrm{2} \\ $$$$\Rightarrow{x}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +...\right)=\mathrm{1}\:{or}\:\mathrm{2} \\ $$$$\:{x}<\mathrm{1} \\ $$$$\frac{{x}}{\mathrm{1}−{x}}=\mathrm{1}\:{or}\:\mathrm{2} \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}}\:{or}\:\frac{\mathrm{2}}{\mathrm{3}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com