Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 47543 by maxmathsup by imad last updated on 11/Nov/18

solve (1+ix)^n =n with x unknown real and n integr natural .

$${solve}\:\left(\mathrm{1}+{ix}\right)^{{n}} ={n}\:\:\:{with}\:{x}\:{unknown}\:{real}\:{and}\:{n}\:{integr}\:{natural}\:. \\ $$

Answered by arcana last updated on 11/Nov/18

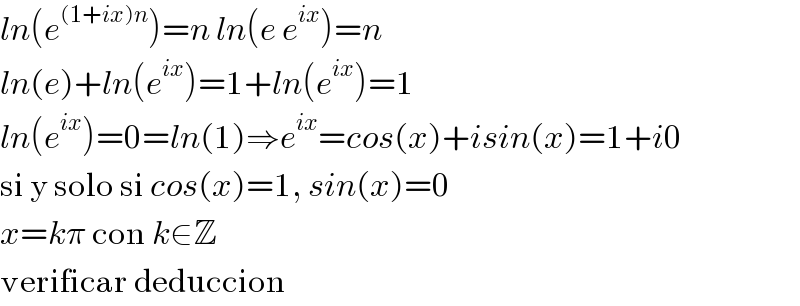
ln(e^((1+ix)n) )=n ln(e e^(ix) )=n ln(e)+ln(e^(ix) )=1+ln(e^(ix) )=1 ln(e^(ix) )=0=ln(1)⇒e^(ix) =cos(x)+isin(x)=1+i0 si y solo si cos(x)=1, sin(x)=0 x=kπ con k∈Z verificar deduccion

$${ln}\left({e}^{\left(\mathrm{1}+{ix}\right){n}} \right)={n}\:{ln}\left({e}\:{e}^{{ix}} \right)={n} \\ $$$${ln}\left({e}\right)+{ln}\left({e}^{{ix}} \right)=\mathrm{1}+{ln}\left({e}^{{ix}} \right)=\mathrm{1} \\ $$$${ln}\left({e}^{{ix}} \right)=\mathrm{0}={ln}\left(\mathrm{1}\right)\Rightarrow{e}^{{ix}} ={cos}\left({x}\right)+{isin}\left({x}\right)=\mathrm{1}+{i}\mathrm{0} \\ $$$$\mathrm{si}\:\mathrm{y}\:\mathrm{solo}\:\mathrm{si}\:{cos}\left({x}\right)=\mathrm{1},\:{sin}\left({x}\right)=\mathrm{0} \\ $$$${x}={k}\pi\:\mathrm{con}\:{k}\in\mathbb{Z} \\ $$$$\mathrm{verificar}\:\mathrm{deduccion} \\ $$

Commented by Smail last updated on 11/Nov/18

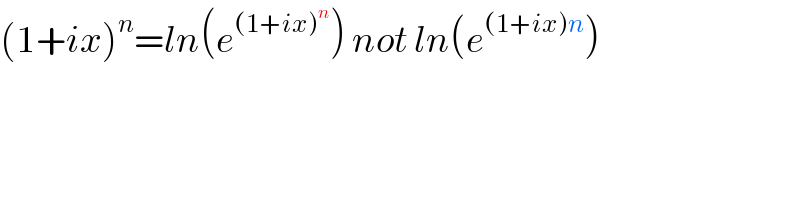
(1+ix)^n =ln(e^((1+ix)^n ) ) not ln(e^((1+ix)n) )

$$\left(\mathrm{1}+{ix}\right)^{{n}} ={ln}\left({e}^{\left(\mathrm{1}+{ix}\right)^{{n}} } \right)\:{not}\:{ln}\left({e}^{\left(\mathrm{1}+{ix}\right){n}} \right) \\ $$$$ \\ $$

Answered by Smail last updated on 11/Nov/18

(1+ix)^n =ne^(2ikπ) with k=(0,1,2,...,n−1) 1+ix=(n)^(1/n) e^((2ikπ)/n) 1+ix=(n)^(1/n) cos(((2kπ)/n))+i(n)^(1/n) sin(((2kπ)/n)) (n)^(1/n) cos(((2kπ)/n))=1 and (n)^(1/n) sin(((2kπ)/n))=x ((2kπ)/n)=cos^(−1) ((1/(n)^(1/n) )) +2mπ with m∈IN x=(n)^(1/n) sin(cos^(−1) ((1/(n)^(1/n) ))+2mπ) =(n)^(1/n) (√(1−(1/(n^2 )^(1/n) )))=(√((n^2 )^(1/n) −1)) x=(√((n^2 )^(1/n) −1))

$$\left(\mathrm{1}+{ix}\right)^{{n}} ={ne}^{\mathrm{2}{ik}\pi} \:\:{with}\:{k}=\left(\mathrm{0},\mathrm{1},\mathrm{2},...,{n}−\mathrm{1}\right) \\ $$$$\mathrm{1}+{ix}=\sqrt[{{n}}]{{n}}{e}^{\frac{\mathrm{2}{ik}\pi}{{n}}} \\ $$$$\mathrm{1}+{ix}=\sqrt[{{n}}]{{n}}{cos}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)+{i}\sqrt[{{n}}]{{n}}{sin}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right) \\ $$$$\sqrt[{{n}}]{{n}}{cos}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)=\mathrm{1}\:{and}\:\:\sqrt[{{n}}]{{n}}{sin}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)={x} \\ $$$$\frac{\mathrm{2}{k}\pi}{{n}}={cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt[{{n}}]{{n}}}\right)\:+\mathrm{2}{m}\pi\:{with}\:\:{m}\in{IN} \\ $$$${x}=\sqrt[{{n}}]{{n}}{sin}\left({cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt[{{n}}]{{n}}}\right)+\mathrm{2}{m}\pi\right) \\ $$$$=\sqrt[{{n}}]{{n}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\sqrt[{{n}}]{{n}^{\mathrm{2}} }}}=\sqrt{\sqrt[{{n}}]{{n}^{\mathrm{2}} }−\mathrm{1}} \\ $$$${x}=\sqrt{\sqrt[{{n}}]{{n}^{\mathrm{2}} }−\mathrm{1}} \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com