
Question Number 156119 by Ghaniy last updated on 08/Oct/21
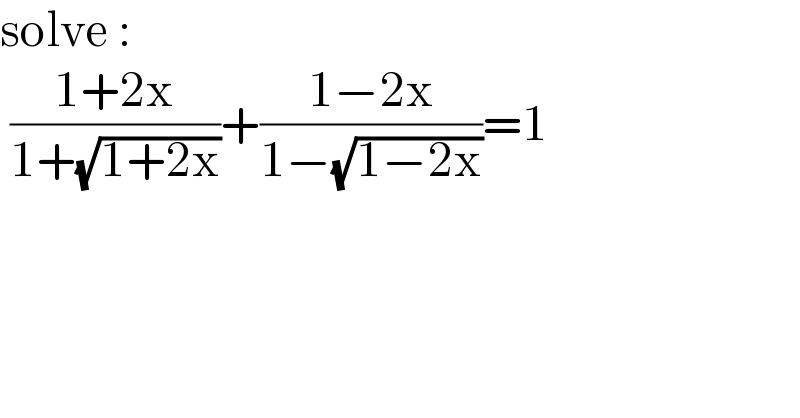
$$\mathrm{solve}\:: \\ $$$$\:\frac{\mathrm{1}+\mathrm{2x}}{\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2x}}}+\frac{\mathrm{1}−\mathrm{2x}}{\mathrm{1}−\sqrt{\mathrm{1}−\mathrm{2x}}}=\mathrm{1} \\ $$$$ \\ $$
Commented by immortel last updated on 08/Oct/21

Commented by Ghaniy last updated on 12/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Answered by MJS_new last updated on 08/Oct/21

$$\mathrm{defined}\:\mathrm{for}\:−\frac{\mathrm{1}}{\mathrm{2}}\leqslant{x}<\mathrm{0}\vee\mathrm{0}<{x}\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{let}\:{t}=\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{2}{x}}\:\Rightarrow\:{t}\geqslant\mathrm{1}\:\Leftrightarrow\:{x}=\frac{{t}\left({t}−\mathrm{2}\right)}{\mathrm{2}} \\ $$$${x}\neq\mathrm{0}\:\Rightarrow\:{t}\neq\mathrm{0}\wedge{t}\neq\mathrm{2} \\ $$$$\mathrm{insert}\:\Rightarrow \\ $$$$\frac{\left({t}−\mathrm{1}\right)^{\mathrm{2}} }{{t}}−\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{\mathrm{1}−\sqrt{−{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}}=\mathrm{1} \\ $$$$\frac{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}{\mathrm{1}−\sqrt{−{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}}=−\frac{{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}}{{t}} \\ $$$$\frac{\mathrm{1}−\sqrt{−{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}}{{t}^{\mathrm{2}} −\mathrm{2}{t}−\mathrm{1}}=−\frac{{t}}{{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}} \\ $$$$\sqrt{−{t}^{\mathrm{2}} +\mathrm{2}{t}+\mathrm{1}}=−\frac{\mathrm{3}{t}^{\mathrm{3}} −\mathrm{3}{t}^{\mathrm{2}} +\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{3}{t}+\mathrm{1}} \\ $$$$\mathrm{squaring}\:\&\:\mathrm{transforming} \\ $$$${t}^{\mathrm{6}} −\mathrm{7}{t}^{\mathrm{5}} +\frac{\mathrm{35}}{\mathrm{2}}{t}^{\mathrm{4}} −\mathrm{18}{t}^{\mathrm{3}} +\mathrm{6}{t}^{\mathrm{2}} =\mathrm{0} \\ $$$${t}^{\mathrm{2}} \left({t}−\mathrm{2}\right)^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{3}{t}+\frac{\mathrm{3}}{\mathrm{2}}\right)=\mathrm{0} \\ $$$${t}\neq\mathrm{0}\wedge{t}\neq\mathrm{2}\wedge{t}\geqslant\mathrm{1}\:\Rightarrow \\ $$$${t}=\frac{\mathrm{3}+\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow \\ $$$${x}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$
Commented by Ghaniy last updated on 12/Oct/21
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
