
Question Number 126266 by bramlexs22 last updated on 18/Dec/20
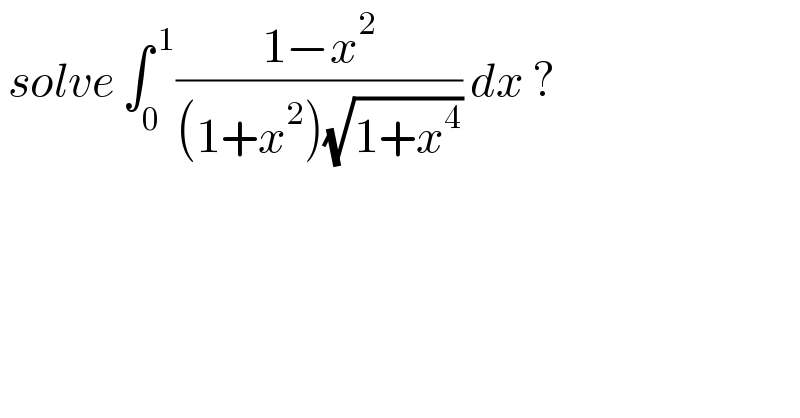
$$\:{solve}\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}−{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}\:{dx}\:?\: \\ $$
Answered by liberty last updated on 19/Dec/20
![N=∫_0 ^( 1) ((x^2 (−1+(1/x^2 )))/(x(x+(1/x))(√(x^2 ((1/x^2 )+x^2 ))))) dx N=∫_0 ^( 1) ((−1+(1/x^2 ))/((x+(1/x))(√((x+(1/x))^2 −((√2))^2 )))) dx [ put x+(1/x)=w→ { ((w=1)),((w=∞)) :}] N=∫_∞ ^( 1) ((−1)/(w(√(w^2 −((√2))^2 )))) dw N=∫_1 ^( ∞) (dw/(w(√(w^2 −((√2))^2 )))) = (1/( (√2))) [arcsec ((w/( (√2)))) ]_1 ^∞ N=(1/( (√2)))((π/2)−(π/4))= (π/(4(√2)))](Q126268.png)
$${N}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{{x}^{\mathrm{2}} \left(−\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right)}{{x}\left({x}+\frac{\mathrm{1}}{{x}}\right)\sqrt{{x}^{\mathrm{2}} \left(\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+{x}^{\mathrm{2}} \right)}}\:{dx} \\ $$$${N}=\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{−\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}{\left({x}+\frac{\mathrm{1}}{{x}}\right)\sqrt{\left({x}+\frac{\mathrm{1}}{{x}}\right)^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}\:{dx} \\ $$$$\left[\:{put}\:{x}+\frac{\mathrm{1}}{{x}}={w}\rightarrow\begin{cases}{{w}=\mathrm{1}}\\{{w}=\infty}\end{cases}\right]\: \\ $$$${N}=\int_{\infty} ^{\:\mathrm{1}} \frac{−\mathrm{1}}{{w}\sqrt{{w}^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}\:{dw}\: \\ $$$${N}=\int_{\mathrm{1}} ^{\:\infty} \frac{{dw}}{{w}\sqrt{{w}^{\mathrm{2}} −\left(\sqrt{\mathrm{2}}\right)^{\mathrm{2}} }}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\left[\mathrm{arcsec}\:\left(\frac{{w}}{\:\sqrt{\mathrm{2}}}\right)\:\right]_{\mathrm{1}} ^{\infty} \\ $$$${N}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}\right)=\:\frac{\pi}{\mathrm{4}\sqrt{\mathrm{2}}} \\ $$
Commented by bramlexs22 last updated on 19/Dec/20

$$\underset{\bigstar} {\underbrace{{waw}.....\checkmark\:\heartsuit}} \\ $$
