
Question Number 25317 by ibraheem160 last updated on 08/Dec/17
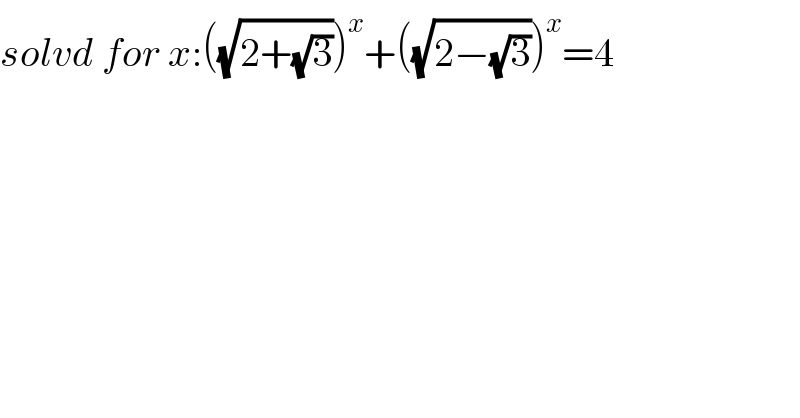
$${solvd}\:{for}\:{x}:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} +\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{4} \\ $$
Answered by ajfour last updated on 08/Dec/17
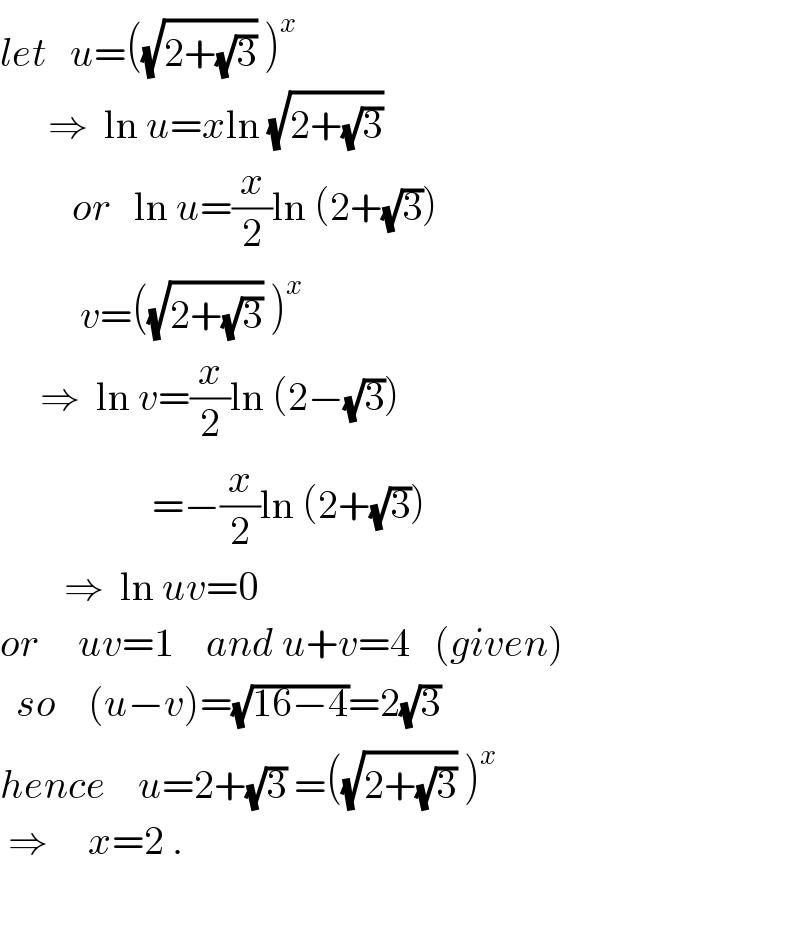
$${let}\:\:\:{u}=\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{{x}} \\ $$$$\:\:\:\:\:\:\Rightarrow\:\:\mathrm{ln}\:{u}={x}\mathrm{ln}\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:\:\:\:\:\:{or}\:\:\:\mathrm{ln}\:{u}=\frac{{x}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{v}=\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{{x}} \\ $$$$\:\:\:\:\:\Rightarrow\:\:\mathrm{ln}\:{v}=\frac{{x}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=−\frac{{x}}{\mathrm{2}}\mathrm{ln}\:\left(\mathrm{2}+\sqrt{\mathrm{3}}\right) \\ $$$$\:\:\:\:\:\:\:\:\Rightarrow\:\:\mathrm{ln}\:{uv}=\mathrm{0} \\ $$$${or}\:\:\:\:\:{uv}=\mathrm{1}\:\:\:\:{and}\:{u}+{v}=\mathrm{4}\:\:\:\left({given}\right) \\ $$$$\:\:{so}\:\:\:\:\left({u}−{v}\right)=\sqrt{\mathrm{16}−\mathrm{4}}=\mathrm{2}\sqrt{\mathrm{3}} \\ $$$${hence}\:\:\:\:{u}=\mathrm{2}+\sqrt{\mathrm{3}}\:=\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{{x}} \\ $$$$\:\Rightarrow\:\:\:\:\:{x}=\mathrm{2}\:. \\ $$$$\:\:\:\:\:\:\:\:\: \\ $$
Answered by Rasheed.Sindhi last updated on 08/Dec/17
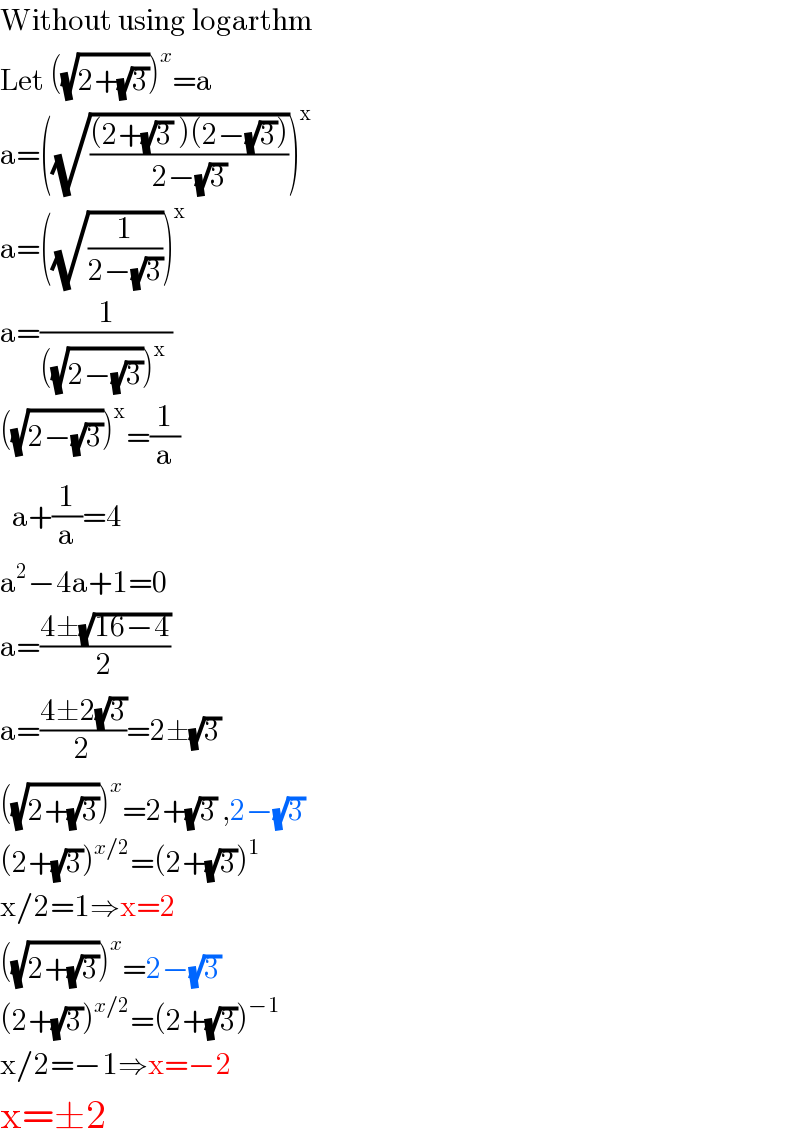
$$\mathrm{Without}\:\mathrm{using}\:\mathrm{logarthm} \\ $$$$\mathrm{Let}\:\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{a} \\ $$$$\mathrm{a}=\left(\sqrt{\frac{\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\mathrm{2}−\sqrt{\mathrm{3}}}}\right)^{\mathrm{x}} \\ $$$$\mathrm{a}=\left(\sqrt{\frac{\mathrm{1}}{\mathrm{2}−\sqrt{\mathrm{3}}}}\right)^{\mathrm{x}} \\ $$$$\mathrm{a}=\frac{\mathrm{1}}{\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{\mathrm{x}} \:} \\ $$$$\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{\mathrm{x}} =\frac{\mathrm{1}}{\mathrm{a}} \\ $$$$\:\:\mathrm{a}+\frac{\mathrm{1}}{\mathrm{a}}=\mathrm{4} \\ $$$$\mathrm{a}^{\mathrm{2}} −\mathrm{4a}+\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{a}=\frac{\mathrm{4}\pm\sqrt{\mathrm{16}−\mathrm{4}}}{\mathrm{2}} \\ $$$$\mathrm{a}=\frac{\mathrm{4}\pm\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{2}}=\mathrm{2}\pm\sqrt{\mathrm{3}} \\ $$$$\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{2}+\sqrt{\mathrm{3}}\:,\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}/\mathrm{2}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\mathrm{1}} \\ $$$$\mathrm{x}/\mathrm{2}=\mathrm{1}\Rightarrow\mathrm{x}=\mathrm{2} \\ $$$$\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{{x}} =\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{{x}/\mathrm{2}} =\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{−\mathrm{1}} \\ $$$$\mathrm{x}/\mathrm{2}=−\mathrm{1}\Rightarrow\mathrm{x}=−\mathrm{2} \\ $$$$\mathrm{x}=\pm\mathrm{2} \\ $$
