
Question Number 167696 by bounhome last updated on 23/Mar/22
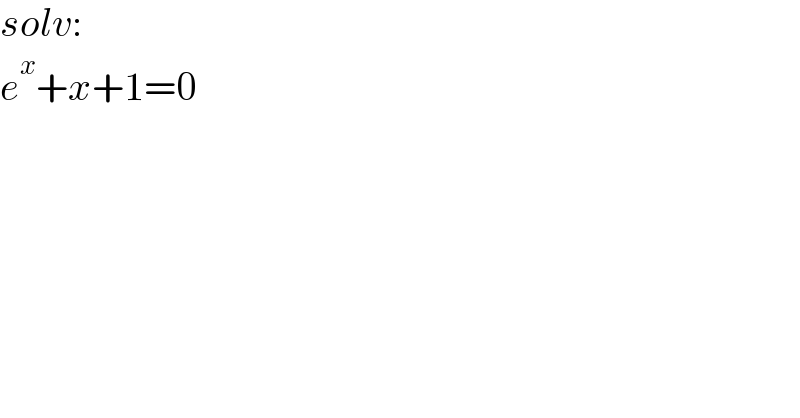
$${solv}:\:\: \\ $$$${e}^{{x}} +{x}+\mathrm{1}=\mathrm{0} \\ $$
Answered by mr W last updated on 23/Mar/22
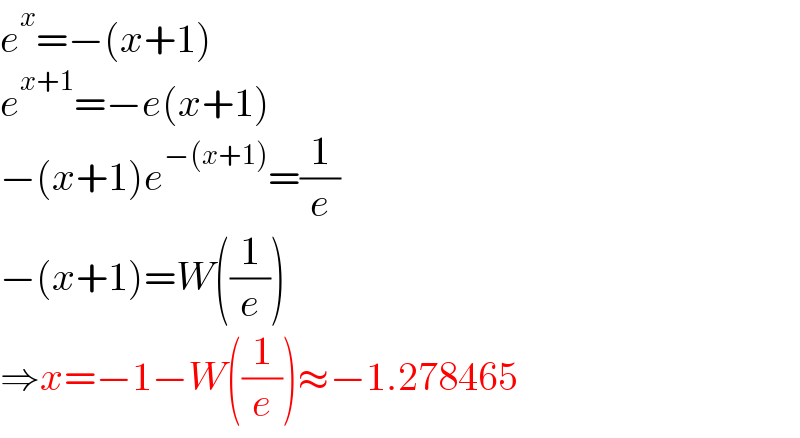
$${e}^{{x}} =−\left({x}+\mathrm{1}\right) \\ $$$${e}^{{x}+\mathrm{1}} =−{e}\left({x}+\mathrm{1}\right) \\ $$$$−\left({x}+\mathrm{1}\right){e}^{−\left({x}+\mathrm{1}\right)} =\frac{\mathrm{1}}{{e}} \\ $$$$−\left({x}+\mathrm{1}\right)={W}\left(\frac{\mathrm{1}}{{e}}\right) \\ $$$$\Rightarrow{x}=−\mathrm{1}−{W}\left(\frac{\mathrm{1}}{{e}}\right)\approx−\mathrm{1}.\mathrm{278465} \\ $$
Commented by essojean last updated on 25/Mar/22
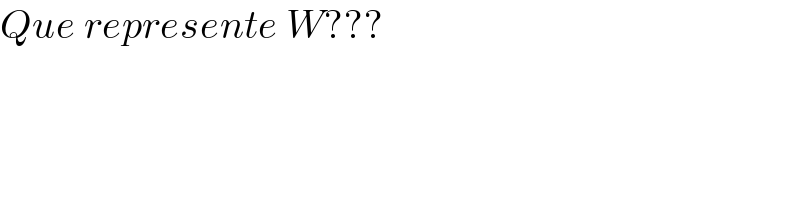
$${Que}\:{represente}\:{W}??? \\ $$
Commented by mr W last updated on 25/Mar/22
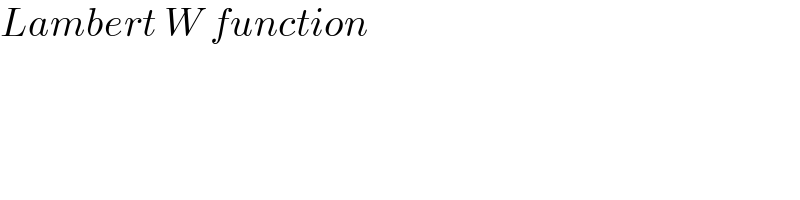
$${Lambert}\:{W}\:{function} \\ $$
